Démontrer le problème n°1 du théorème de Thébault

[Amg5f5gh]

Bonjour,
J'ai trouvé une démonstration du problème n°1 du théorème de thebault mais je n'arrive pas à démontrer la rotation de centre O et d'angle 90° qui transforme C en D, B en D'.
https://fr.m.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Th%C3%A9bault#:~:text=Le%20probl%C3%A8me%20de%20Th%C3%A9bault%20no%202%20est%20un%20probl%C3%A8me,par%20exemple%20ABL%20et%20BCM.

Comment démontrer cette rotation, svp?

[catamat]

Bonjour

Cela provient du fait que les angles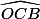 et sont de même mesure, d'après une propriété du parallélogramme.

On en déduit que r(B)=D' car la rotation conserve les angles et les longueurs... (à détailler bien sûr)

[Ben314]

Salut,
La rotation vectorielle de 90° envoie sur donc envoie sur .

[Amg5f5gh]

Merci pour vos messages mais ça ne démontre pas ma rotation de centre o et d angle 90°. Ça démontre l'image de B par cette rotation est D'.

[Amg5f5gh]

Comment démontrer la rotation de centre O et d'angle 90° ? D'où vient-elle ?

[catamat]

On définit ou on utilise cette rotation par son centre O et son angle Pi/2
Ce type de ration est fort utile dans un carré de centre O puisqu'elle envoie un sommet sur le sommet suivant (ici dans le sens direct)

[Ben314]

Personnellement, ce que je ne comprend pas, c'est ce que peut bien signifier de "démontrer une rotation" . . .

Ce qu'on démontre (ou pas...), c'est une propriété, c'est à dire quelque chose qui est soit vrai, soit faux (par exemple une égalité, une inégalité, une appartenance, etc . . .), mais de "démontrer une application" (en l’occurrence une rotation), ça n'a aucun sens ! ! !

Bref, est-ce que tu peut poser ta question avec une phrase qui veut dire quelque chose ?

[Amg5f5gh]

Dans la démonstration, on utilise la rotation de centre O et d'angle 90° pour démontrer que C à pour image D et B à pour image D'.
... Donc, N a pour image P.
Sauf que démontrer cela sans avoir démontrer qu'il s'agissait bien d'une rotation de centre O et d'angle de 90° est imprécis. Et je ne sais pas comment démontrer (montrer d'où vient cette rotation de centre O et d'angle 90°)

[Ben314]

Sauf que démontrer cela sans avoir démontrer qu'il s'agissait bien d'une rotation de centre O et d'angle de 90° est imprécis. . .

Je comprend rien : de quel "il" parle tu ?

Là, ce qu'on fait, c'est qu'on regarde quel sont les images de certains points par une certaine rotation.
Il n'y a absolument pas à démontrer que je sais pas quelle application est une rotation.
Si je te dit de prendre un marteau (pour enfoncer un clou), est ce que tu as l'impression qu'il y a à démontrer que l'objet que tu va prendre est bien un marteau ? Soit tu as fait ce que je dit et c'est bien un marteau, soit tu as rien compris et c'est pas un marteau, mais il y a bien évidement rien à "démontrer" . . .
Ben là, c'est exactement pareil : on te dit de prendre la rotation de centre O et d'angle 90° puis de vérifier des trucs. Donc si ce que tu prend, c'est pas la rotation en question, tout ce que ça veut dire, ben c'est que tu sait pas lire . . .

[Amg5f5gh]

Dites ça à mon professeur de mathématiques qui me demande de démontrer cette rotation.

[catamat]

Bonjour

Je n'ai rien à ajouter à ce qu'à dit Ben314, on ne démontre pas une rotation, on utilise ses propriétés qui ont été vues et démontrées en cours.

Si ton prof a dit cela c'était un raccourci, il voulait dire démontrer que l'on peut utiliser une rotation.
Cela signifie que l'on définit d'abord la rotation r (centre et angle) et ensuite on démontre que r(C) =D et r(B)=D'.

[Ben314]

Dites ça à mon professeur de mathématiques qui me demande de démontrer cette rotation.

Hummm.....
En ce qui me concerne, j'ai comme qui dirait "un doute notoire" concernant le fait qu'un prof. de math puisse prononcer (à jeun) une telle absurdité.

Et ça serait pas idiot, à un moment donné, de comprendre que les maths, c'est pas du charabia sans queue ni tête mais des trucs qui sont sensés vouloir dire quelque chose.