Demonstration en trigonométrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
fodediarra11s
- Membre Naturel
- Messages: 36
- Enregistré le: 17 Mai 2012, 20:27
-
 par fodediarra11s » 17 Mai 2012, 20:42
par fodediarra11s » 17 Mai 2012, 20:42
s'il vs plait j'ai besoin d'un coup de main pour ce exo
DDémontrer que cos4x +sin^3 x - 2 =0
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 20:53
par Dinozzo13 » 17 Mai 2012, 20:53
Salut !
En supposant que l'équation est
+\sin^3 (x) -2 =0)
ce n'est pas toujours vrai :
pour x=0 : cos4x +sin^3 x - 2= -1
-
fodediarra11s
- Membre Naturel
- Messages: 36
- Enregistré le: 17 Mai 2012, 20:27
-
 par fodediarra11s » 17 Mai 2012, 21:28
par fodediarra11s » 17 Mai 2012, 21:28
Merci je pensais à sa c'est ds camarades qui me l'ont donné donc je voulais avoir l'esprit clair
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 21:31
par Dinozzo13 » 17 Mai 2012, 21:31
Au pire, pour leur clouer le bec direct, trace-leur la courbe représentative de
+\sin^3(x)-2)
et montre que cette fonction n'est jamais constamment nulle :++:
-
fodediarra11s
- Membre Naturel
- Messages: 36
- Enregistré le: 17 Mai 2012, 20:27
-
 par fodediarra11s » 17 Mai 2012, 21:34
par fodediarra11s » 17 Mai 2012, 21:34
Dinozzo13 a écrit:Salut !
En supposant que l'équation est
+\sin^3 (x) -2 =0)
ce n'est pas toujours vrai :
pour x=0 : cos4x +sin^3 x - 2= -1
comment démontrer l'égalité suivante
+\cos(b)+\cos(c) = 1+\4sin(a/2)sin(b/2)sin(c/2))
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 21:38
par Dinozzo13 » 17 Mai 2012, 21:38
Elle à l'air cool, mais ce n'est qu'une égalité, pas une démonstration.
-
fodediarra11s
- Membre Naturel
- Messages: 36
- Enregistré le: 17 Mai 2012, 20:27
-
 par fodediarra11s » 17 Mai 2012, 21:39
par fodediarra11s » 17 Mai 2012, 21:39
fodediarra11s a écrit: comment démontrer l'égalité suivante
a,b,c sont les angles en radians d'un triangle .
+\cos(b)+\cos(c) = 1+\4sin(a/2)sin(b/2)sin(c/2))
là tout vérifie que l'égalité est vraie
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 21:40
par Dinozzo13 » 17 Mai 2012, 21:40
En effet, cette égalité est vraie quels que soient les réels a,b,c :++:
-
fodediarra11s
- Membre Naturel
- Messages: 36
- Enregistré le: 17 Mai 2012, 20:27
-
 par fodediarra11s » 17 Mai 2012, 21:40
par fodediarra11s » 17 Mai 2012, 21:40
Dinozzo13 a écrit:Elle à l'air cool, mais ce n'est qu'une égalité, pas une démonstration.
je me suis po bien expliquer dsl mais il sagit de démontrer
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 21:42
par Dinozzo13 » 17 Mai 2012, 21:42
Tu veux donc démontrer cette formule. Une idée ?
-
fodediarra11s
- Membre Naturel
- Messages: 36
- Enregistré le: 17 Mai 2012, 20:27
-
 par fodediarra11s » 17 Mai 2012, 21:45
par fodediarra11s » 17 Mai 2012, 21:45
Dinozzo13 a écrit:Tu veux donc démontrer cette formule. Une idée ?
exact Monsieur
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 21:46
par Dinozzo13 » 17 Mai 2012, 21:46
C'est ça ton idée :ptdr: ?
-
fodediarra11s
- Membre Naturel
- Messages: 36
- Enregistré le: 17 Mai 2012, 20:27
-
 par fodediarra11s » 17 Mai 2012, 21:48
par fodediarra11s » 17 Mai 2012, 21:48
Dinozzo13 a écrit:C'est ça ton idée :ptdr: ?
dsl je pensais passer par les formules de simpson mais sa m mène ........
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 21:55
par Dinozzo13 » 17 Mai 2012, 21:55
Oui, on peut faire comme ça :++:
Dans un premier temps, j'aurai montrer que cos(a)+cos(b)+cos(c)=cos(a)+cos(b)-cos(a+b) puis que
1+4sin(a/2)sin(b/2)sin(c/2)=cos(a)+cos(b)-cos(a+b)
-
fodediarra11s
- Membre Naturel
- Messages: 36
- Enregistré le: 17 Mai 2012, 20:27
-
 par fodediarra11s » 17 Mai 2012, 22:20
par fodediarra11s » 17 Mai 2012, 22:20
Dinozzo13 a écrit:Oui, on peut faire comme ça :++:
Dans un premier temps, j'aurai montrer que cos(a)+cos(b)+cos(c)=cos(a)+cos(b)-cos(a+b) puis que
1+4sin(a/2)sin(b/2)sin(c/2)=cos(a)+cos(b)-cos(a+b)
j'arrive po à m'ensortir
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 22:36
par Dinozzo13 » 17 Mai 2012, 22:36
Déjà, pour démontrer que :
cos(a)+cos(b)+cos(c)=cos(a)+cos(b)-cos(a+b)
ça va ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 22:39
par Dinozzo13 » 17 Mai 2012, 22:39
fodediarra11s a écrit:a,b,c sont les angles en radians d'un triangle
.
Remarque :
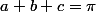
:++:
-
fodediarra11s
- Membre Naturel
- Messages: 36
- Enregistré le: 17 Mai 2012, 20:27
-
 par fodediarra11s » 17 Mai 2012, 23:51
par fodediarra11s » 17 Mai 2012, 23:51
Dinozzo13 a écrit:Déjà, pour démontrer que :
cos(a)+cos(b)+cos(c)=cos(a)+cos(b)-cos(a+b)
ça va ?
non mais je peux si vs m l'expliquez
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Mai 2012, 00:15
par Dinozzo13 » 18 Mai 2012, 00:15
Si
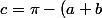)
alors
+\cos(b)+\cos(c)= ...)
.
-
fodediarra11s
- Membre Naturel
- Messages: 36
- Enregistré le: 17 Mai 2012, 20:27
-
 par fodediarra11s » 18 Mai 2012, 00:19
par fodediarra11s » 18 Mai 2012, 00:19
Dinozzo13 a écrit:Si
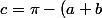)
alors
+\cos(b)+\cos(c)= ...)
.
c'est clair mais je vois tjrs pas la route qui me mène car je trouve cos(a+b)=cosacosb-sinasinb
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
