Démonstration

par **rmax505** » 16 Fév 2006, 18:20

Bonjour
En utilisant 3a=a+2a comment peut-on montrer que sin(3a)=sina(4cos²a-1) ???

SVP ! C'est casse tête depuis 2h :marteau:

par **leibniz** » 16 Fév 2006, 18:21

Salut,

Utilise les formules de transformation.........

par **Asuka** » 16 Fév 2006, 18:22

c'est dans quel chapitre qu'on te demande ça ? parce que je crois me rapeller que dans un chapitre on peux utiliser une formule pour trouver ça, mais je suis pas sur.

par **rmax505** » 16 Fév 2006, 18:26

je pense qu'il faut utiliser la relation sin²acosb+sinbcos²b

par **Asuka** » 16 Fév 2006, 18:31

voilà je pensais à cette formule, bah je pense que si tu fais ça tu peux trouver, nan?

par **rmax505** » 16 Fév 2006, 18:35

est ce que vous pouvez développer l'équation:
sin2acosa+sinacos2a ?
merci d'avance

par **leibniz** » 16 Fév 2006, 18:37

Salut,

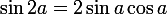
et

C'est du cours.....

A+

par **fonfon** » 16 Fév 2006, 18:39

Salut,

est ce que vous pouvez développer l'équation:
sin2acosa+sinacos2a ?
merci d'avance

essaies avec

cos2a=cos²a-sin²a=2cos²a-1=1-2sin²a
sin2a=2sinacosa

fais des essais avec les differentes formules tu verras situ trouves quelques chose de correct

par **leibniz** » 16 Fév 2006, 18:41

Messages croisés fonfon....

par **rmax505** » 16 Fév 2006, 18:50

c'est bon j'ai trouvé il suffisé de mettre en facteur sina merci bcp a tous

par **fonfon** » 16 Fév 2006, 18:54

oui ,Leibniz ca m'arrive souvent aussi :ptdr:

par **allomomo** » 16 Fév 2006, 19:00

Salut,

par **leibniz** » 16 Fév 2006, 19:01

Salut, allomomo,

On a déjà parlé des solution toutes faites :hum:

par **leibniz** » 16 Fév 2006, 19:02

En plus, c'est déjà reglé!!........

par **allomomo** » 16 Fév 2006, 19:04

Salut,

.......

Une autre manière de le démontrer :

par **rmax505** » 16 Fév 2006, 19:04

arpès suite à cela je dois prouver que x=4cos²a-1 et que x-1=(4cos²a-1)/(2cosa)
comment fait-on ?

par **allomomo** » 16 Fév 2006, 19:05

Bon j'ai censuré la moitié,

J'avais un problème lorsque je voulais poster quelqu'un est responsable de ca? lol

par **allomomo** » 16 Fév 2006, 19:07

Que veut tu faire avec ca ? C'est extrait d'un grand enoncé ...

rmax505 a écrit:arpès suite à cela je dois prouver que x=4cos²a-1 et que x-1=(4cos²a-1)/(2cosa)
comment fait-on ?

par **leibniz** » 16 Fév 2006, 19:08

Est ce que t'as lu la discussion avant de répondre?!

par **rmax505** » 16 Fév 2006, 19:12

Les triangles ABC et CBD sont isocèles DB=1 DC=x BC=x DA=1 L'ange BAD=5a
ABC=a et ACB=a aussi
1-Donner une valeur de a en radians
2-Determiner une mesure de chachun des angles BÂD , ADB et ABD en fonction de a
3- Calculer AB et AC en focntion de x
4-En utilisant la règle des sinus , établir que
(sin(3a)/x)=sin a et que (sin(3a)/(x-1))=sin(2a)

5-En utilisant 3a=a+2a , établir que sin(3a)=sina(4cos²a-1)
6-En déduire que x=4cos²a-1 et que x-1=(4cos²a-1)/(2cosa)
7- Démontrer finalement que cos pi/7 est solution de l'équation 8X^3 - 4X² - 4X + 1 = 0

Ile ne me reste plus que les deux dernières questions et j'aurai fini l'exercice

Démonstration

Démonstration

re

re

Qui est en ligne