Démonstration sur les limites des suite.

[fpaco]

Bonjour, j'aurais une question à propo d'une propriété sur les suites sur les suites.

Voici la propriété : Soit (Un) une suite convergeant vers l, alors le suite (Un+k) converge aussi vers l (avec k un entier naturel)

Bien que ce résultat soit évident je n'arrive pas à trouver une démonstration rigoureuse.
Je pense que il faut s'appuyer sur la définition mais je n'ai pas réussi à la bidouillé pour obtenir le résultat.
Pourriez vous m'aider svp?
merci

[hdci]

Je pense que il faut s'appuyer sur la définition

Oui, tout à fait.
La définition est
)

Et vous voulez démontrer

)

Si pour tout l'inégalité est obtenue, que pouvez-vous dire de par rapport à ? Déduisez-en une valeur ("suffisante") pour

[mathelot]

bonsoir,

écris la convergence de la suite avec des epsilons et des quantificateurs

[fpaco]

On a n+k >=no+k>=no
Mais je ne vois pas où ca nous mène.

[hdci]

On sait que si 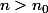alors
On sait que si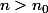 alors

Par conséquent que peut-on dire de ?

Pour rappel, dans la définition de la limite que j'ai écrite ;

)

l'hypothèse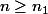 est une condition suffisante : à aucun moment on ne doit trouver le "meilleur 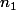possible", il suffit d'en trouver un. On en déduit que si on prend 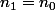, que se passe-t-il ?