Bonsoir, j'aurai une petite question à propos d'une démonstration que j'ai vu en cour.
Cependant je ne la comprend pas très bien. Pourriez vous m'aider svp .
Voici de quoi il est question :
Soit une suite (Un) a termes positifs convergeant vers l supérieur ou égale à 0
Si la suite (Un) tend vers l , alors la suite ((Un)^(1/2)) converge vers l^(1/2)
Preuve : Comme (Un converge vers l, il existe un naturel N tel que pour tout n supérieur ou égale à N,
lUn- l l inférieur ou égale à E
donc l (Un^(1/2))^2 - (l^(1/2))^2 l inférieur ou égale à E
Donc l Un^(1/2) -l^(1/2) l inférieur ou égale à E/(lUn^(1/2) +l^(1/2) )
A ce moment la, il faut distinguer 2 cas l>0 et l=0 mais je ne comprend pas pourquoi.
merci de votre aide
Ps je suis désolé pour toutes les puissances 1/2 mais je ne sais pas comment écrire les racines carrés.
Démonstration sur les limites des suite.
6 messages
- Page 1 sur 1
Re: Démonstration sur les limites des suite.
Donc l Un^(1/2) -l^(1/2) l inférieur ou égale à E/(lUn^(1/2) +l^(1/2) )
si Un = 0 pour tout n, on ne peut pas diviser
si Un = 0 pour tout n, on ne peut pas diviser
Re: Démonstration sur les limites des suite.
pascal16 a écrit:si Un = 0 pour tout n, on ne peut pas diviser
en fait il suffit que
(Exemple, la suite
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Démonstration sur les limites des suite.
Ok mais par conséquent comment je peut démontrer le cas où l=0 ?
Re: Démonstration sur les limites des suite.
Il faut écrire alors directement
 donc
donc
)
(Remarquer que la suite étant positive on peut s'afranchir des valeurs absolues ici)
Et on veut montrer
)
Il s'agit donc de trouver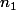
(J'ai utilisé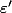 dans la seconde proposition, pour éviter toute confusion avec le
dans la seconde proposition, pour éviter toute confusion avec le  de la première, vu qu'évidemment on va se servir de la première, mais que le
de la première, vu qu'évidemment on va se servir de la première, mais que le  qu'on utilisera dans la première ne sera pas le même que dans la seconde... Une fois qu'on a bien compris comment cela marchait, on peut se passer de cet artifice).
qu'on utilisera dans la première ne sera pas le même que dans la seconde... Une fois qu'on a bien compris comment cela marchait, on peut se passer de cet artifice).
(Remarquer que la suite étant positive on peut s'afranchir des valeurs absolues ici)
Et on veut montrer
Il s'agit donc de trouver
(J'ai utilisé
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Démonstration sur les limites des suite.
Le but est d'expliquer la correction de l'exo
lUn- l l inférieur ou égale à E
comme Un et l sont positif, on a (Un^(1/2))^2 =Un et (l^(1/2))^2
donc l (Un^(1/2))^2 - (l^(1/2))^2 l inférieur ou égale à E
donc | (Un^(1/2)) - (l^(1/2)) |*[(Un^(1/2)) + (l^(1/2))] <=E
| (Un^(1/2)) - (l^(1/2)) |* (Un^(1/2)) + | (Un^(1/2)) - (l^(1/2)) |(l^(1/2)) <=E
donc
| (Un^(1/2)) - (l^(1/2)) |(l^(1/2)) ≤ E
là, si l=0 ne permet pas de conclure
sinon
| (Un^(1/2)) - (l^(1/2)) | ≤ E/(l^(1/2))
et on a un bon candidat, il fallait prend E*(l^(1/2))
lUn- l l inférieur ou égale à E
comme Un et l sont positif, on a (Un^(1/2))^2 =Un et (l^(1/2))^2
donc l (Un^(1/2))^2 - (l^(1/2))^2 l inférieur ou égale à E
donc | (Un^(1/2)) - (l^(1/2)) |*[(Un^(1/2)) + (l^(1/2))] <=E
| (Un^(1/2)) - (l^(1/2)) |* (Un^(1/2)) + | (Un^(1/2)) - (l^(1/2)) |(l^(1/2)) <=E
donc
| (Un^(1/2)) - (l^(1/2)) |(l^(1/2)) ≤ E
là, si l=0 ne permet pas de conclure
sinon
| (Un^(1/2)) - (l^(1/2)) | ≤ E/(l^(1/2))
et on a un bon candidat, il fallait prend E*(l^(1/2))
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
