Démonstration par récurrence

[Ghostbuster]

Bonjour!
Avec les épreuves pratiques de mathématiques, on doit travailler sur tableur. J'ai eu en exo ce sujet. J'ai déjà fait la partie sur excel, et j'en suis arrivée à : Vn = n² - 1. On sait que Vn = 3Un donc on déduit facilement que Un = (n² -1)/3.
La question 2.(c) me demande de démontrer l'expression de Un en fonction de n que l'on a déduit de ce T.P. Sur le net, il y a des corrigés mais je ne les comprends pas et ils ne vont pas dans la même direction que moi (enfin ce que je pense). Je pensais donc vérifier cette expression au rang n=1, puis au rang k pour k un entier naturel non nul, mais après je suis bloquée.
Si quelqu'un veut bien se pencher sur le problème et me guider parce que là je commence à tout mélanger! Merci d'avance.

[Luc]

Salut,

Il semble que tu veux montrer l'égalité suivante:



pour tout entier n supérieur ou égal à 1, par récurrence sur n.

Je pensais donc vérifier cette expression au rang n=1, puis au rang k pour k un entier naturel non nul.

C'est la bonne méthode mais c'est pas tout à fait ça.
Effectivement il faut vérifier l'égalité pour n=1 (c'est l'initialisation).
Ensuite, il faut montrer que si l'égalité est vraie à un certain rang fixé , alors elle l'est au rang (c'est l'hérédité ).
Tu peux alors conclure grâce au principe de récurrence.

Indice pour l'hérédité.
Tu supposes qu'à un certain rang n,
est vraie.
Tu veux montrer que est vraie.


et

[Ghostbuster]

Merci pour la réponse. Alors je vais poster ce que je pensais faire :
Je vérifie la propriété P au rang n=1
= = 0

et là je dois comparer cette valeur à ce que j'ai trouvé dans mon tableur ? c'est à dire ce que j'ai trouvé par la relation de départ = ?
Quoiqu'il en soit, est vraie.

Mon hypothèse de récurrence :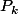 est vraie pour k un entier naturel non nul =
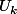donc je prends le rang supérieur
= et je vais devoir me servir de l'hypothèse de récurrence ?
Je sens que la réponse est évidente mais je ne vois pas...

[Luc]

Merci pour la réponse. Alors je vais poster ce que je pensais faire :
Je vérifie la propriété P au rang n=1
= = 0

et là je dois comparer cette valeur à ce que j'ai trouvé dans mon tableur ? c'est à dire ce que j'ai trouvé par la relation de départ = ?
Quoiqu'il en soit, est vraie.

Mon hypothèse de récurrence : est vraie pour k un entier naturel non nul =
donc je prends le rang supérieur
= et je vais devoir me servir de l'hypothèse de récurrence ?
Je sens que la réponse est évidente mais je ne vois pas...

Oui c'est ça, il faut montrer que =

en utilisant l'hypothèse de récurrence = .

Il faut donc faire apparaître l'expression à partir de celle-ci: .

Tu y es presque!

[Ghostbuster]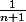

x ...
donc euh..
x ?

:triste:
Même si on me dit la réponse, je crois que j'ai un véritable problème de compréhension ^_^

[Luc]

Salut,

Il faut que tu montres que



en utilisant l'hypothèse de récurrence, qui te dit:



Reprends les calculs calmement, ça devrait passer :we:

[Ghostbuster]

= n
= n (1 + )
= n (1 + x ) d'après l'hypothèse de récurrence
= n (1 + )
= n ()
=
=


Je crois que j'ai enfin réussi... :we:

[Luc]

= n (1 + )
= n (1 + x ) d'après l'hypothèse de récurrence
= n (1 + )
= n ()
=
=


Je crois que j'ai enfin réussi... :we:

Bravo!
Juste deux détails: la première égalité est fausse, mais à partir de la deuxième ligne c'est vrai. Je suppose que c'est une faute de frappe.
Une autre faute de frappe à la fin: c'est bien et non

En tout cas bravo d'avoir trouvé!

[Ghostbuster]

J'ai oublié un signe + entre le "n" et la somme, c'est cela?
En effet c'est une faute de frappe, je n'ai pas encore la main pour les insertions de formules bien que j'ai acquis un bon niveau depuis ces deux heures...
En tout cas merci de votre aide et de vos encouragements ^^
À bientôt.