Démonstration par récurrence

[Le Chat]

hello les matheux

j'ai du mal à saisir le principe d'induction... :doh:

Il faut démontrer que 1+2+3+...+n = n(n+1)/2 par récurrence

On sait que c'est vrai pour n=1. Puis, je suppose que P(m) est vrai et je vérifie pour P(m+1), mais là je bloque à 1+2+3+...+(m+1)

:marteau:

___________________
Cicéron, c'est Poincaré!

[Carpate]

hello les matheux

j'ai du mal à saisir le principe d'induction... :doh:

Il faut démontrer que 1+2+3+...+n = n(n+1)/2 par récurrence

On sait que c'est vrai pour n=1. Puis, je suppose que P(m) est vrai et je vérifie pour P(m+1), mais là je bloque à 1+2+3+...+(m+1)

:marteau:
__________________
Cicéron, c'est Poincaré!

Où est le probléme ?
Hypothése : vraie au rang n :
On veut montrer que

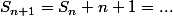
Tu ne sais pas réduire au même dénominateur ?

[Le Chat]

Où est le probléme ?
Hypothése : vraie au rang n :
On veut montrer que

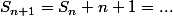
Tu ne sais pas réduire au même dénominateur ?

Merci, c'est cela que je cherchais
Je ne sais pas pourquoi

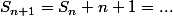
D'ailleurs je n'ai presque aucune notion de suite. Mais je sais comment réduire au même dénominateur! :ptdr:

[Kikoo <3 Bieber]

Merci, c'est cela que je cherchais
Je ne sais pas pourquoi

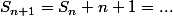
D'ailleurs je n'ai presque aucune notion de suite. Mais je sais comment réduire au même dénominateur! :ptdr:

Salut,

Tu peux "voir" cette formule récursive en écrivant u_{n+1} sous forme sommatoire.

[Carpate]

Merci, c'est cela que je cherchais
Je ne sais pas pourquoi

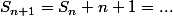
D'ailleurs je n'ai presque aucune notion de suite. Mais je sais comment réduire au même dénominateur! :ptdr:

Donc tu sais calculer et obtenir ainsi :

[Le Chat]

Oui bon. Je vais utiliser cette formule tout bêtement pour démontrer par récurrence.
À part ça, j'ai de la misère à comprendre les définitions formelles de voisinage et de limite dans mon bouquin...


:zen:

[kalyster]

Oui bon. Je vais utiliser cette formule tout bêtement pour démontrer par récurrence.
À part ça, j'ai de la misère à comprendre les définitions formelles de voisinage et de limite dans mon bouquin...


:zen:

Chat c'est pas drôle :zen: