Démonstration par récurrence et déduction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Aya
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Juin 2016, 16:12
-
 par Aya » 05 Nov 2016, 19:35
par Aya » 05 Nov 2016, 19:35
Bonsoir tout le monde, j'ai passé une évaluation ce matin,et j'avais pas pu répondu à la dernière question de cet exercice.. Prière de m'aider

1- Montrer que: ∀ n ∈ IN * (1+α)ⁿ ≥ 1+n α où α ∈ R+ (c'est facile; j'ai opté pour la récurrence)
2- En déduire que :
a- ∀ n ∈ IN * 3ⁿ > n
b- ∀ n ∈ IN * (n+1)ⁿ ≥ 2nⁿ
Bonne soirée à tous, et merci d'avance!
Modifié en dernier par
Aya le 05 Nov 2016, 21:12, modifié 1 fois.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 05 Nov 2016, 19:47
par Pseuda » 05 Nov 2016, 19:47
Bonsoir,
Fais
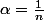
dans la 1ère formule.
-
Aya
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Juin 2016, 16:12
-
 par Aya » 05 Nov 2016, 19:56
par Aya » 05 Nov 2016, 19:56
Oui c'est vrai, mais c'était demandé de montrer la 1ère formule en optant pour la récurrence, j'ai su le faire c'était quand même facile, mais j'ai bloqué sur les autres !
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 05 Nov 2016, 20:11
par Pseuda » 05 Nov 2016, 20:11
"Fais
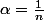
dans la 1ère formule", c'était pour répondre à la dernière question de l'exercice, soit la 2b, celle où, si j'ai bien compris, tu as bloqué.
-
Aya
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Juin 2016, 16:12
-
 par Aya » 05 Nov 2016, 20:35
par Aya » 05 Nov 2016, 20:35
Ahh... J'ai remplacé, mais je n'ai trouvé que : (1+1/n)^n ≥ 1
Celà voudrait-il dire quoi ?
Ps: D'ailleurs j'avais bloqué sur la 2a aussi

-
Aya
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Juin 2016, 16:12
-
 par Aya » 05 Nov 2016, 21:09
par Aya » 05 Nov 2016, 21:09
J'ai pris : α=1⁄n
J'ai obtenu après remplacement : (1+1/n)ⁿ ≥ 1
((n+1)/n)ⁿ = [ (n+1)ⁿ / n ⁿ ] ≥ 1
D'où : (n+1)ⁿ ≥ n ⁿ (car leur quotient est ≥ 1)
Mais on m'a demandé de démontrer que : (n+1)ⁿ ≥ 2n ⁿ ???
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 06 Nov 2016, 11:41
par Pseuda » 06 Nov 2016, 11:41
Aya a écrit:J'ai pris : α=1⁄n
J'ai obtenu après remplacement : (1+1/n)ⁿ ≥ 1
((n+1)/n)ⁿ = [ (n+1)ⁿ / n ⁿ ] ≥ 1
D'où : (n+1)ⁿ ≥ n ⁿ (car leur quotient est ≥ 1)
Mais on m'a demandé de démontrer que : (n+1)ⁿ ≥ 2n ⁿ ???
Bonjour,
Il y a une erreur dans ton calcul. Normalement tu dois trouver la bonne formule.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 06 Nov 2016, 12:14
par zygomatique » 06 Nov 2016, 12:14
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Aya
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Juin 2016, 16:12
-
 par Aya » 06 Nov 2016, 13:23
par Aya » 06 Nov 2016, 13:23
Bonjour tout le monde,
Je ne vois pas encore le chemin que je dois suivre.. J'ai refais le calcul mais je n'ai trouvé que :
^{n}\geq n^{n})
Aidez-moi svp ...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 06 Nov 2016, 13:55
par zygomatique » 06 Nov 2016, 13:55
il y a un deux ou pas ?
parce que ton inégalité (n + 1)^n > n^n est triviale (quand n > 0)
et je t'ai répondu ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Nov 2016, 14:30
par Ben314 » 06 Nov 2016, 14:30
Partant de ça :
Aya a écrit: (1+α)ⁿ ≥ 1+n α
Si tu prend α=1/n, ça serait pas idiot de le faire
des deux cotés de l'inégalité et pas uniquement dans la partie gauche :
Aya a écrit:Ahh... J'ai remplacé, mais je n'ai trouvé que : (1+1/n)^n ≥ 1
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Aya
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Juin 2016, 16:12
-
 par Aya » 06 Nov 2016, 16:01
par Aya » 06 Nov 2016, 16:01
Je vais remplacer

par

uniquement dans le côté gauche, comme l'a recommandé Ben314 :
^{n} \geq 1+n\alpha)
^{n}\times n^{n} \geq n^{n} (1+n\alpha ))
 \right]^{n} \geq n^{n}+n\times n^{n}\times \alpha)
Or
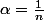
 \right]^{n} \geq 2n^{n})
C.Q.F.D
FINALEMENT !!!! Je l'ai trouvé.. C'était pas trop facile à voir quand même !
Merci beaucoup les gens


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Nov 2016, 16:48
par Ben314 » 06 Nov 2016, 16:48
Je me suis peut-être mal exprimé, mais moi, justement, j'avais plutôt dit de remplacer des deux cotés...
Enfin, bon, le principal, c'est que tu ait obtenu le bon résultat...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 06 Nov 2016, 17:28
par zygomatique » 06 Nov 2016, 17:28
Aya a écrit:Je vais remplacer

par

uniquement dans le côté gauche, comme l'a recommandé Ben314 :
^{n} \geq 1+n\alpha)
^{n}\times n^{n} \geq n^{n} (1+n\alpha ))
 \right]^{n} \geq n^{n}+n\times n^{n}\times \alpha)
Or
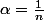
 \right]^{n} \geq 2n^{n})
C.Q.F.D
FINALEMENT !!!! Je l'ai trouvé.. C'était pas trop facile à voir quand même !
Merci beaucoup les gens

c'est surtout que tu as mélangé deux méthodes (celle de ben314 et la mienne) ce qui alourdit les choses
avec ce que je propose :
^n = \left[n \left(1 + \dfrac 1 n \right) \right]^n = n^n (1 + 1/n)^n \ge n^n(1 + n * 1/n) = n^n * 2)
tout simplement ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Nov 2016, 17:48
par Ben314 » 06 Nov 2016, 17:48
Même pas vrai que c'est moi : c'est Pseuda dans le premier Post...
Pseuda a écrit:Fais
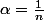
dans la 1ère formule.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 06 Nov 2016, 17:56
par zygomatique » 06 Nov 2016, 17:56
oui ... pas eu envie de remonter à l'auteur initial ... qui ne nous en voudra pas ... je l'espère !!

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 06 Nov 2016, 18:00
par Pseuda » 06 Nov 2016, 18:00
Bonsoir,
@ zygomatique @Ben314
Bien sûr que non, je ne vous en veux pas, en tout cas, pas à Ben314 !

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités

par
uniquement dans le côté gauche, comme l'a recommandé Ben314 :
C.Q.F.D
dans la 1ère formule.
