Demonstration par réccurence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 26 Aoû 2006, 15:21
par krokos55 » 26 Aoû 2006, 15:21
bonjour j'ai besoin de votre aide car il me faut démontrer par réccurence que pour tt n dans IN on a :
3^(3n+2) + 2^(n+4) est divisible par 5
merci de votre aide
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 26 Aoû 2006, 16:08
par nada-top » 26 Aoû 2006, 16:08
salut,
alors pour

on a
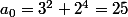
donc la la proposition est vérifiée .
- maintenant supposons que
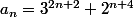
est dévisible par 5 donc

- démontrons que
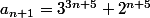
est divisible par 5 .
donc on
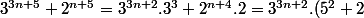 +2^{n+4}.2 <br /><br />= 5^2 .3^{3n+2} +2.(3^{3n+2}+2^{n+4}) <br />= 5^2 .3^{3n+2} + 2(5k) = 5( 5.3^{3n+2} + 2k ) = 5 k')
avec

alors

est divisible par 5 .
enfin selon la proprité de réccurence on peut en déduire que

est dévisible par 5.
@+
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 26 Aoû 2006, 16:51
par aviateurpilot » 26 Aoû 2006, 16:51
sans reccurence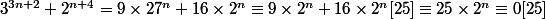
donc

est meme divisible par
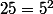
sauf erreur
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 26 Aoû 2006, 18:57
par krokos55 » 26 Aoû 2006, 18:57
merci à vous deux.... mais il me fallait une démonstration par réccurence !
en revanche pourriez vous me donner un coup de main car je dois determiner la valeur de :
Sigma (k.( k parmis n )) pour k allant de 1 à n sans utiliser la derivation mais en s'aidant de la formule ci dessous qui est à démontrer
la formule : k.(k parmis n) = n.(k-1 parmis n-1)
j'ai démontré la forùmule avec des factoriels mais je suis perdu pour la suite.
je sais juste que le résultat vaut n.2^(n-1) car avec la dérivation cela donne ca.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 19:02
par nekros » 26 Aoû 2006, 19:02
Il faut montrer que
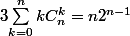
, c'est ça, sans la dérivation ?
A+
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 26 Aoû 2006, 19:16
par nada-top » 26 Aoû 2006, 19:16
salut ,
tu as démontré que
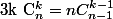
donc :
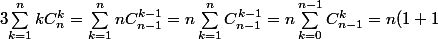^{n-1} = n.2^{n-1})
Edit : Nekros--- K allant de 1 à n .
@+
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 26 Aoû 2006, 19:34
par krokos55 » 26 Aoû 2006, 19:34
pourquoi est ce que Sigma des (k parmis n-1) pour k allant de 0 à n-1 est égal à (1+1) ^(n-1)
et pourquoi décales tu du rang (0 à n) à (1 à n-1)
merci de m'éclairer
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 19:36
par nekros » 26 Aoû 2006, 19:36
C'est le binôme de Newton.
Nada-top essaie de se ramener à la forme
^N=\sum_{k=0}^N C_N^k a^k b^{N-k})
Pour la deuxième question, où est-ce que tu vois ça ?
A+
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 26 Aoû 2006, 19:46
par krokos55 » 26 Aoû 2006, 19:46
pardon je voulais dire de (1 à n) à (0 à n-1)
est ce parce que le binôme fonctionne a partir du rang 0 ?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 26 Aoû 2006, 19:54
par nada-top » 26 Aoû 2006, 19:54
Re
pour ta 2eme question : on a
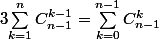
c'est la meme chose . (essaie par des valeurs simples et tu verra )
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 19:55
par nekros » 26 Aoû 2006, 19:55
C'est pour se ramener à la forme que j'ai écrite.
Ici,
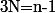
A+
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 26 Aoû 2006, 20:10
par krokos55 » 26 Aoû 2006, 20:10
pourquoi changes tu si c'est la même chose ?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 26 Aoû 2006, 20:21
par nada-top » 26 Aoû 2006, 20:21
pour se ramener à la forme du binome Newton (regarde le post de Nekros )
alors dans notre cas
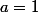
et
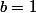
et
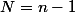
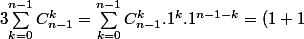^{n-1}= 2^{n-1})
c'est clair?
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 27 Aoû 2006, 10:25
par krokos55 » 27 Aoû 2006, 10:25
parfaitement clair merci beaucoup à vous tous !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
