Démonstration formule binome de newton

[nythostyle]

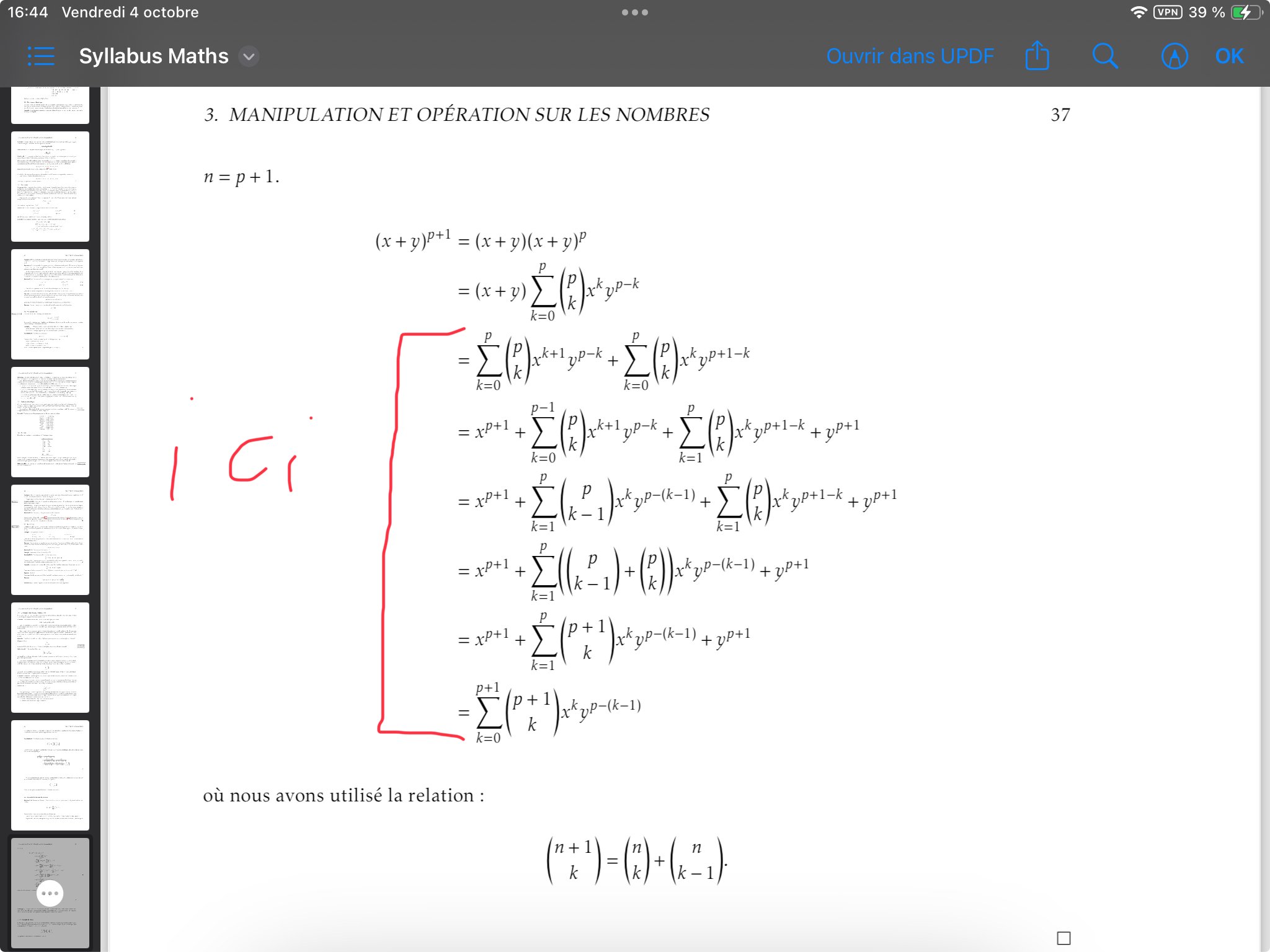
Bonjour, j ai un peu de mal avec la notation sommatoire en particulier dans la démonstration du binôme de newton je ne comprends pas la succession des étapes précédant le marqueur rouge et la 1 ere etape àpd marqueur rouge

[nythostyle]

Je réalise que j'ai fait une erreur dans ma rédaction, c'est plutôt de la 1 ère à la 2 ème étape dans l'encadré où je ne comprends pas tout à fait le procédé

[capitaine nuggets]

Salut !

En distribuant on a



Or le but va être de rassembler ces deux sommes et pour n'en faire qu'une. Pour cela, il faudrait avoir des exposants en et "similaires" dans les deux sommes.

En effectuant le changement de variable dans la première somme , on a

.

Sous cette forme, on a bien une "correspondance" des exposants avec la seconde somme

,

néanmoins, les deux sommes ne commencent et ne finissent pas au même indice. Qu'à cela ne tienne, il suffit de sortir ce qui est "en trop" de façon à avoir deux somme sur les mêmes indices. On va donc sortir dans le terme d'indice 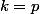et dans le terme d'indice 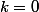. On a



et

,

donc

.

En utilisant la formule du triangle de Pascal (rappelée dans ton scan), il te reste alors seulement à identifier lequel parmi les deux termes et , peut-être "réintégré" dans la somme sous la forme du terme d'indice 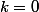et d'indice 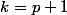, pour finalement avoir

.

[catamat]

Bonjour
Ce que l'on appelle développer ou factoriser est l'utilisation de cette formule :



Attention toutefois ne doit pas dépendre de l'indice k
(ce qui est le cas ici, x ne dépend pas de k)

[nythostyle]

Salut !

En distribuant on a



Or le but va être de rassembler ces deux sommes et pour n'en faire qu'une. Pour cela, il faudrait avoir des exposants en et "similaires" dans les deux sommes.

En effectuant le changement de variable dans la première somme , on a

.

Sous cette forme, on a bien une "correspondance" des exposants avec la seconde somme

,

néanmoins, les deux sommes ne commencent et ne finissent pas au même indice. Qu'à cela ne tienne, il suffit de sortir ce qui est "en trop" de façon à avoir deux somme sur les mêmes indices. On va donc sortir dans le terme d'indice et dans le terme d'indice . On a



et

,

donc

.

En utilisant la formule du triangle de Pascal (rappelée dans ton scan), il te reste alors seulement à identifier lequel parmi les deux termes et , peut-être "réintégré" dans la somme sous la forme du terme d'indice et d'indice , pour finalement avoir

.

Je te remercie mille fois !!! J'aurais pas pu obtenir une explication plus claire , merci à catamat également pour le rappel de la formule qui se trouve dans mon cours mais que j'ai manifestement eu du mal à mettre en pratique.

[nythostyle]

Je profite de ce post pour passer un petit message à qui pourrait me venir en aide, je cherche un bon cours sur les combinatoires avec des exercices et un bon module théorique je trouve les indications théoriques dans mon syllabus un peu trop abstraites et pas très orienté exos

[capitaine nuggets]

Le problème au lycée, c'est qu'on n'a pas toujours les bonnes notions pour justifier correctement les choses dans le domaine de l'analyse combinatoire. On se contente de "faire avec les mains" et on essaie de faire appel au "bon sens". A priori il faudra soit chercher sur le net, soit nous poser des questions sur le sujets. Mais je conçois que ce cours ne soit pas facile à comprendre de prime abord.

[vam]

Bonjour

je ne sais pas si c'est quelque chose de ce genre que tu cherches, cela correspond à l'enseignement lycée qu'on faisait, sans fioritures
https://www.maths-et-tiques.fr/telech/20Combi.pdf

[nythostyle]

Merci, vam ! C'est le genre de ressource que je cherchais oui

[mathou13]

Bonjour,

Pour le passage de la 1ere étape à la seconde il développe x^a×x^b=x^(a+b) idem pour y

Pour illustrer les combinatoire:
https://www.google.com/url?sa=t&source= ... wt8qXad7et
https://www.google.com/url?sa=t&source= ... ZD-uYhXZQ_
https://www.google.com/url?sa=t&source= ... ZD-uYhXZQ_

Cordialement.