Bonjour, je fais des exercices pour m'entrainer et je bloque sur l'un d'eux :
1) montrer que acosx+bsinx= re[(a-ib)e^ix]
(là je pensais utiliser e^ix= cosx+isinx ?
2) z=a+ib, r module de z et a argument de z, montrer que
acosx+bsinx=r(cos(x-a)
(là je pensais partir de r(cos(x-a) et développer: r(cosxcosa+sinxsina)?
3) Determinez tous les réels x de [-pi,pi]tels que cosx-sqrt(3)sinx (inférieur ou égal) à 1
(je pensais utiliser la formule du dessus et l'appliquer a cox-sqrt(3)sinx pour avoir : 2(cos(x+pi/3)
merci d'avance de votre aide:)
Démonstration : complexes en trigonométrie
6 messages
- Page 1 sur 1
Bonjours
1)
en effet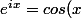 + isin(x)) donc
donc
e^{ix} = a cos(x) + bsin(x) + aisin(x) - ibcos(x)) (simple développement)
(simple développement)
Il suffit de prenre la parti réelle pour avoir le résultat.
pour le second,
donc d'après le résultat précédent, + bsin(x) = Re(\overline{z}e^{ix} ))
Or
Il suffit de faire le produit des deux complexe avec l'exponnentielle et de repasser sous forme trigo puis prendre la partie réelle.
Enfin pour le dernier tu es sur la bonne piste, il faut résoudre l'équation avec la seconde formule.
1)
en effet
Il suffit de prenre la parti réelle pour avoir le résultat.
pour le second,
donc d'après le résultat précédent,
Or
Il suffit de faire le produit des deux complexe avec l'exponnentielle et de repasser sous forme trigo puis prendre la partie réelle.
Enfin pour le dernier tu es sur la bonne piste, il faut résoudre l'équation avec la seconde formule.
Kiocle a écrit:Bonjours
1)
en effetdonc
(simple développement)
Il suffit de prenre la parti réelle pour avoir le résultat.
pour le second,
donc d'après le résultat précédent,
Or
Il suffit de faire le produit des deux complexe avec l'exponnentielle et de repasser sous forme trigo puis prendre la partie réelle.
Enfin pour le dernier tu es sur la bonne piste, il faut résoudre l'équation avec la seconde formule.
Merci beaucoup !! j'ai bien compris pour les deux premières questions, et pour la dernière je trouve comme résultat:
cos(x+pi/3)(inferieur ou egal a ) cos(pi/3)
donc x=0 ou x=-2pi/3 ?
est-ce bien cela? encore merci !!
MarieLi a écrit:Merci beaucoup !! donc quand il y a une inégalité je dois prendre dans les solutions les bornes de l'intervalle?
Tu prend toute les solution qui vérifient l'inégalité, donc comme tu a inférieur ou "égal", la solution 0 est dans l'intervalle et -2pi/3 aussi. Sinon il suffirait d'exclure avec des intervalle ouvert.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
