Démonstration avec théorème de la bijection
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 18 Oct 2006, 15:39
par Baba » 18 Oct 2006, 15:39
Mais vu qu'il faut que je prouve que mon équation admet une unique solution ...
Il faut que j'utilise le théorème de la bijection. Non ??
Mais pour pouvoir l'utiliser, il faut que je prouve que la fonction est strictement monotone...
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 18 Oct 2006, 16:48
par Zebulon » 18 Oct 2006, 16:48
Oui, et pour montrer qu'une fonction est strictement monotone sur un intervalle, on étudie le signe de...?
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 18 Oct 2006, 17:23
par Baba » 18 Oct 2006, 17:23
de f', sa dérivé quoi ...
que je suis bête quand je m'y met ....
C'est bien ca quand même ??!!?
(Que je continue pas à me ridiculiser un peu plus ...)
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 18 Oct 2006, 17:29
par Zebulon » 18 Oct 2006, 17:29
Non, non, vous ne vous ridiculisez pas, c'est bien ça. Et même si ça avait été faux, vous n'auriez pas été ridicule pour autant.
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 18 Oct 2006, 17:34
par Baba » 18 Oct 2006, 17:34
Non mais le truc, c'est que tout ca je le sais !!!!
Et en plus souvent ca ne me pose pas problème !
Mais il y a aussi des fois ou je bloque très bêtement sur des trucs que je pourrais voir tout de suite ....
Bref, merci beaucoup de votre aide :++: :king2:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 18 Oct 2006, 17:36
par Zebulon » 18 Oct 2006, 17:36
Baba a écrit:Mais il y a aussi des fois ou je bloque très bêtement sur des trucs que je pourrais voir tout de suite ....
Le mieux pour vaincre ça, c'est... de faire des exos.
A bientôt! :we:
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 18 Oct 2006, 19:34
par Baba » 18 Oct 2006, 19:34
={-1\over2\sqrt x})
Au fait quelqu'un peut me dire si la dérivée, c'est bien ca ??
(je vous redonne la fonction que je dois alors dériver:
={5-\sqrt x (x-2))
)
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 21 Oct 2006, 14:52
par Baba » 21 Oct 2006, 14:52
J'aurais besoin d'une confirmation:
La dérivée de
={5-\sqrt x (x-2))
Est-ce bien
={-(x-2)\over2\sqrt x})
??
Merci d'avance pour vos réponses !
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 21 Oct 2006, 17:20
par Zebulon » 21 Oct 2006, 17:20
Posez
=\sqrt x)
et
=(x-2))
. Déterminez alors la dérivée de u(x).v(x) puis celle de f(x).
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 21 Oct 2006, 17:37
par Baba » 21 Oct 2006, 17:37
Ouais, bon moi j'ai pris
={5\over(x-2)}-\sqrt x)
La dérivée de ca, est-ce bien
={-5\over(x-2)^2}-{1\over2\sqrt x})
??
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 21 Oct 2006, 17:44
par Zebulon » 21 Oct 2006, 17:44
Baba a écrit:Ouais, bon moi j'ai pris
={5\over(x-2)}-\sqrt x)
La dérivée de ca, est-ce bien
={-5\over(x-2)^2}-{1\over2\sqrt x})
??
1). Ceci est faux : la dérivée de
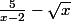
est
}^2}+{1\over{2\sqrt x}})
.
2). Pourquoi calculer cette dérivée?
=5-\sqrt x(x-2)\neq {5\over{x-2}}-\sqrt x)
!!!
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 21 Oct 2006, 18:05
par Baba » 21 Oct 2006, 18:05
Non non mais c'est pour autre chose.
Pourquoi la dérivée c'est ca:
=-{5\over{(x-2)}^2}+{1\over2\sqrt x})
La dérivée de
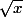
je croyais que c'était
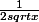
Ce serait
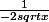
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
