Demande d'exercices sur les dérivées

[Anonyme]

Bonjour,

Alors, en fait on vient de commencer le chapitre des dérivées en classe, et donc j'aimerais bien qu'on me donne quelques exercices pour que je m'entraîne à en faire...

Des exercices niveau débutante, parce qu'on est qu'au début du chapitre, je n'ai donc pas assez de connaissances encore ;)

Voilà, je vous remercie d'avance! :happy3:
J'espère que je vais réussir à faire vos exercices :lol3:


(PS: je risque de ne pas voir de suite vos réponses, je n'ai pas tout le temps l'ordinateur de libre --' ... Mais je vous répondrais dès que je pourrai :) )

[antonyme]

Bonjour,

Alors, en fait on vient de commencer le chapitre des dérivées en classe, et donc j'aimerais bien qu'on me donne quelques exercices pour que je m'entraîne à en faire...

Des exercices niveau débutante, parce qu'on est qu'au début du chapitre, je n'ai donc pas assez de connaissances encore

Voilà, je vous remercie d'avance! :happy3:
J'espère que je vais réussir à faire vos exercices :lol3:


(PS: je risque de ne pas voir de suite vos réponses, je n'ai pas tout le temps l'ordinateur de libre --' ... Mais je vous répondrais dès que je pourrai )

Salut!
Voici quelque fonctions à dériver (de plus en plus dûr :lol3: continu tant que tu à vu la méthode en cours et dis moi si tu as vu des dérivés plus dures) :
1- Les bases
f(x) = 23
g(x) = 10x - 2
h(x) = 4x - 6*(2x +3)

2- Dérivées usuelles
i(x) = 5x²+2x-3
j(x) = 1/x + 3x
k(x) =

Je m'arrête là ça m'étonnerait que tu soit allé plus loin (dérivée de produits, quotient, composées). Je ne suis pas sur que tu es déjà vu les fonctions usuelle, dis moi si tu en veut encore.

[Anonyme]

Salut!
Voici quelque fonctions à dériver (de plus en plus dûr :lol3: continu tant que tu à vu la méthode en cours et dis moi si tu as vu des dérivés plus dures) :
1- Les bases
f(x) = 23
g(x) = 10x - 2
h(x) = 4x - 6*(2x +3)

2- Dérivées usuelles
i(x) = 5x²+2x-3
j(x) = 1/x + 3x
k(x) =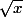

Je m'arrête là ça m'étonnerait que tu soit allé plus loin (dérivée de produits, quotient, composées). Je ne suis pas sur que tu es déjà vu les fonctions usuelle, dis moi si tu en veut encore.

Bonsoir Antonyme!

Je te remercie pour m'avoir donner ces fonctions )
Voici ce que j'ai fait :

1 - Les bases:

f'(x) = 0
g'(x) = 10*1-0 = 10
h'(x) = 4*1-0*(2*1+0) = 4

2- Dérivées usuelles:

i'(x) = (2*5x)+(2*1)-0 = 10x+2
j'(x) = -(1/x)^2 +3
k'(x) = 1/2*\/¯x


Voilà
Je veux bien que tu m'en donnes encore si ça ne te dérange pas ^^
Et non, nous n'en avons pas vu des plus difficile pour l'instant...

Et puis j'ai une question... Lorsqu'on dérive une fonction est-ce qu'il faut préciser du genre " la fonction dérivée de f(x)=..... est f'(x)=...... " ou ce n'est pas la peine?
il y a une présentation "spéciale" à avoir ou pas?
Merci d'avance !

Très bonne soirée, à bientôt!

[maths0]

Bonsoir Antonyme!

Je te remercie pour m'avoir donner ces fonctions )
Voici ce que j'ai fait :

1 - Les bases:

f'(x) = 0
g'(x) = 10*1-0 = 10
h'(x) = 4*1-0*(2*1+0) = 4

2- Dérivées usuelles:

i'(x) = (2*5x)+(2*1)-0 = 10x+2
j'(x) = -(1/x)^2 +3
k'(x) = 1/2*\/¯x


Voilà
Je veux bien que tu m'en donnes encore si ça ne te dérange pas ^^
Et non, nous n'en avons pas vu des plus difficile pour l'instant...

Et puis j'ai une question... Lorsqu'on dérive une fonction est-ce qu'il faut préciser du genre " la fonction dérivée de f(x)=..... est f'(x)=...... " ou ce n'est pas la peine?
il y a une présentation "spéciale" à avoir ou pas?
Merci d'avance !

Très bonne soirée, à bientôt!

Il faut toujours dire sur quelle intervalle la fonction est dérivable.
Sinon rien d'autre en particulier. h'(x) = 4*1-0*(2*1+0) = 4 est fausse.

[Julie_S]

Bonsoir, ma chérie ^^

Alors le nombre dérivé est un nombre tel que pour un réel a de l'ensemble sur lequel cette fonction est dérivable, nous ayons :
avec h et k des constantes réelles. k est alors le nombre dérivé en a que nous appelons .
En généralisant à tout x de l'ensemble sur lequel f est dérivable, soit la fonction f'(x) telle que :
. Cette fonction décrit en quelque sorte la pente de la courbe de manière locale en tout x. Si f'(x) est positif, alors f(x) est croissante, et si f'(x) est d'autant plus importante, alors la pente de f en un endroit proche de x sera d'autant plus prononcée. Le constat est contraire si f'(x) est négative, puis "très négative" aux alentours d'un certain x.

Bien, passons à quelques formules de dérivées à connaître !!

Si f(x)=constante alors f'(x)=0 (cela s'explique de manière graphique : si une courbe prend une valeur constante, c'est-à-dire la même valeur en tout x, alors nous visualisons cela comme une droite parallèle à l'axe des abscisses. La pente d'une telle courbe est évide
Si alors
Si alors
Si alors
Si alors
Si alors
Si alors
Si alors

Toutes ces formules se démontrent avec plus ou moins de complexité grâce à la formule d'au-dessus !

Voilà pour les fonctions de variables

Maintenant, pour les fonctions qui comportent différentes fonctions incluses (somme de fonctions, différence de fonctions, produit de fonctions, etc.), nous allons définir la dérivée et les opérations faisables :
Soient f, u et v trois fonctions numériques quelconques.

Informellement, nous ne notons pas f(x) mais f, pour un soucis de clarté !

Si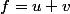 , alors 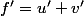donc si 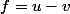alors
Si , alors
Si , alors
Si alors
Si alors
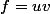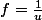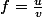Si alors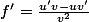

Voilà, j'ai passé en revue l'essentiel de ton cours ^^

Maintenant, pour un peu d'entraînement, dérive les fonctions suivantes :








Au fait, pour la présentation, tu fais comme tu veux Généralement, les profs comprennent d'emblée que quand tu parles de f', il s'agit de la dérivée de f !

A bientôt ma choupette !! Tu me manques :triste: J'espère que mon frère n'est pas trop méchant !! Haha

Julie

[Anonyme]

Bonsoir, ma chérie ^^

Alors le nombre dérivé est un nombre tel que pour un réel a de l'ensemble sur lequel cette fonction est dérivable, nous ayons :
avec h et k des constantes réelles. k est alors le nombre dérivé en a que nous appelons .
En généralisant à tout x de l'ensemble sur lequel f est dérivable, soit la fonction f'(x) telle que :
. Cette fonction décrit en quelque sorte la pente de la courbe de manière locale en tout x. Si f'(x) est positif, alors f(x) est croissante, et si f'(x) est d'autant plus importante, alors la pente de f en un endroit proche de x sera d'autant plus prononcée. Le constat est contraire si f'(x) est négative, puis "très négative" aux alentours d'un certain x.

Bien, passons à quelques formules de dérivées à connaître !!

Si f(x)=constante alors f'(x)=0 (cela s'explique de manière graphique : si une courbe prend une valeur constante, c'est-à-dire la même valeur en tout x, alors nous visualisons cela comme une droite parallèle à l'axe des abscisses. La pente d'une telle courbe est évide
Si alors
Si alors
Si alors
Si alors
Si alors
Si alors
Si alors

Toutes ces formules se démontrent avec plus ou moins de complexité grâce à la formule d'au-dessus !

Voilà pour les fonctions de variables

Maintenant, pour les fonctions qui comportent différentes fonctions incluses (somme de fonctions, différence de fonctions, produit de fonctions, etc.), nous allons définir la dérivée et les opérations faisables :
Soient f, u et v trois fonctions numériques quelconques.

Informellement, nous ne notons pas f(x) mais f, pour un soucis de clarté !

Si , alors donc si alors
Si , alors
Si , alors
Si alors
Si alors
Si alors

Voilà, j'ai passé en revue l'essentiel de ton cours ^^

Maintenant, pour un peu d'entraînement, dérive les fonctions suivantes :








Au fait, pour la présentation, tu fais comme tu veux Généralement, les profs comprennent d'emblée que quand tu parles de f', il s'agit de la dérivée de f !

A bientôt ma choupette !! Tu me manques :triste: J'espère que mon frère n'est pas trop méchant !! Haha

Julie

Ouuuaaouuuh :zen: tu m'as tout mis!! :we:
Merci beaucoup ma chérie!!

Voici les fonctions dérivées:

f'(x) = 0
g'(x) = 23*1 = 23
h'(x) = x+2
i'(x) = 76x^37 - 154x^22

.... j'ai du mal à dériver les fonctions j et k :hum: et je crains que ce soit juste ceux dont j'ai dérivé.. hum hum ...

J'espère que tu passes de bonnes vacances ma belle )
Tu me manques énormément .... :'(

Oh mais, est-ce possible que ton frère soit méchant avec moi??? :ptdr:
Non il est très gentil <3

J'attends ton retour avec I-M-P-A-T-I-E-N-C-E !! (je fais le décompte des jours.... x) )


Allez, à bientôt ma belle !!! :we:
Je te fais plein de bisous de France :*

[Anonyme]

Il faut toujours dire sur quelle intervalle la fonction est dérivable.
Sinon rien d'autre en particulier. h'(x) = 4*1-0*(2*1+0) = 4 est fausse.

Bonjour, merci

Hum.. je ne vois pas mon erreur :hum:

[antonyme]

Bonjour, merci

Hum.. je ne vois pas mon erreur :hum:

6(2x + 3) n'est pas constant! Si tu développe ça donne 12x + 18, c'était le piège :lol3:

f'(x) = 0
g'(x) = 23*1 = 23
h'(x) = x+2
i'(x) = 76x^37 - 154x^22

Les deux premières dérivées sont bonnes mais ensuite tu n'as pas toujours bien employé la formule: (la notation veut dire dérivé de , ça permet de bien voir ce que tu dérive )

-
-

Deux fonctions qui utilise la même méthode pour que tu réessaie (avec un n négatif pour rigoler :we: ):

[Anonyme]

6(2x + 3) n'est pas constant! Si tu développe ça donne 12x + 18, c'était le piège :lol3:


Les deux premières dérivées sont bonnes mais ensuite tu n'as pas toujours bien employé la formule: (la notation veut dire dérivé de , ça permet de bien voir ce que tu dérive )

-
-

Deux fonctions qui utilise la même méthode pour que tu réessaie (avec un n négatif pour rigoler :we: ):

Ahhhh d'accord


Pour les deux autres fonctions j'ai trouvé que leurs dérivées sont :

5*(3x^2-1)-234 = 15x^2

Je sens qu'il y a un piège dans celle-ci :doute2:
Mais bon, ^^ voilà ce que j'ai trouvé :

4*(-5x^-5-1) = -1x^-4

[Julie_S]

Ahhhh d'accord


Pour les deux autres fonctions j'ai trouvé que leurs dérivées sont :

5*(3x^2-1)-234 = 15x^2

Je sens qu'il y a un piège dans celle-ci :doute2:
Mais bon, ^^ voilà ce que j'ai trouvé :

4*(-5x^-5-1) = -1x^-4

Ce n'est pas totalement bon ^^
Pour la première, n'oublie pas de dériver tous les termes !
Pour la deuxième, il faut passer par l'écriture suivante : Mais il est vrai que ce n'est peut-être pas encore un réflexe pour toi. Cela viendra, tu verras !

Julie

[antonyme]

Pour la deuxième, il faut passer par l'écriture suivante :

Ah mais la formule marche aussi bien pour les n positifs que pour les n négatifs (et puis ça fais une formule de moins à apprendre :zen: )

D'ailleurs tu avait bien commencé Saccharine

[Julie_S]

Ah mais la formule marche aussi bien pour les n positifs que pour les n négatifs (et puis ça fais une formule de moins à apprendre :zen: )

D'ailleurs tu avait bien commencé Saccharine

Oui c'est vrai mais je voulais faire passer une autre formule ^^ Comme ça, cela ferait un peu d'entrainement

[Anonyme]

Bonjour :)

Merci à vous deux! :happy2:

[pidou7]

Bonjour, je n'arrive pas à résoudre ce problème, qqun pour m'aider?

"Une classe crée une mini-entreprise pour fabriquer et vendre des bougies à la cire d'abeille. L'élève chargé de la comptabilité estime que les couts fixes (matériel...) s'élève à 60€ et que les couts variables qui dépendent de la quantité q de bougies fabriquées sont :
2,5q - 0,01q² (en euros)
les élènes ne souhaitent pas produire plus de 125bougies
a) Exprimer le cout total ( Ct) de production en fonction du nombre de bougies fabriquées.
b) Quel est le cout moyen ( Cm) des 100 premières bougies produites ?
c) Les économistes désignent par cout marginal ( Cm) le cout engendré par la fabrication d'une unité supplémentaire; on a donc :
Cm (q) = Ct (q+1) - Ct (q)

Calculer Cm (100) c'est-à-dire le supplément de cout engendré par la fabrication de la 101ème bougie.

[Kikoo <3 Bieber]

Thanks to create your own topic please ! :)

[pidou7]

on fait comment ?

[Kikoo <3 Bieber]

on fait comment ?

On the top-right-hand corner, in the lycée section, I suppose ^^

Sh**, on the top-left-hand corner, I mean