Demande d'aide pour un devoir maison
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Paulrubens
- Membre Naturel
- Messages: 20
- Enregistré le: 01 Oct 2016, 18:32
-
 par Paulrubens » 01 Oct 2016, 22:39
par Paulrubens » 01 Oct 2016, 22:39
anthony_unac a écrit:Que vous demande t on dans l'exercice : "Montrer que le discriminant de l'équation précédente vaut Δ= a²+8a-20"
Votre calcul est faux !
Reprenez tout ceci demain à tête reposée ...
d'accord je verrais ceci
-
Paulrubens
- Membre Naturel
- Messages: 20
- Enregistré le: 01 Oct 2016, 18:32
-
 par Paulrubens » 02 Oct 2016, 09:52
par Paulrubens » 02 Oct 2016, 09:52
merci pour votre animation elle m'est utile pour mieux comprendre
-
Paulrubens
- Membre Naturel
- Messages: 20
- Enregistré le: 01 Oct 2016, 18:32
-
 par Paulrubens » 02 Oct 2016, 09:59
par Paulrubens » 02 Oct 2016, 09:59
anthony_unac a écrit:Que vous demande t on dans l'exercice : "Montrer que le discriminant de l'équation précédente vaut Δ= a²+8a-20"
Votre calcul est faux !
donc j'ai x²+x(-4-a)+9=0
Δ= (-4-a)²-4(1)(9)
=16+a²-36
= a² - 20
mais je vois mal comment passer de mon résultat au résultat indiqué
-
Paulrubens
- Membre Naturel
- Messages: 20
- Enregistré le: 01 Oct 2016, 18:32
-
 par Paulrubens » 02 Oct 2016, 10:46
par Paulrubens » 02 Oct 2016, 10:46
quelqu'un pour m'aider s'il vous plait?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 02 Oct 2016, 10:52
par XENSECP » 02 Oct 2016, 10:52
Paulrubens a écrit:quelqu'un pour m'aider s'il vous plait?
Tu peux résumer où tu en es ?
-
Paulrubens
- Membre Naturel
- Messages: 20
- Enregistré le: 01 Oct 2016, 18:32
-
 par Paulrubens » 02 Oct 2016, 11:11
par Paulrubens » 02 Oct 2016, 11:11
XENSECP a écrit: Paulrubens a écrit:quelqu'un pour m'aider s'il vous plait?
Tu peux résumer où tu en es ?
4. On recherche l'intersection de D et P. Quelle équation doit-on résoudre?
5. Montrer que le discriminant de l'équation précédente vaut Δ= a²+8a-20
déterminer les valeurs de a pour lesquelles D et P ont un seul point d'intersection.
pour le 4. j'ai trouvé que la solution était x²+x(-4-a)+9=0 mais le Δ de cette équation n'est pas la même que celle de la question 5. et je n'arrive pas à trouver celle-ci
-
Paulrubens
- Membre Naturel
- Messages: 20
- Enregistré le: 01 Oct 2016, 18:32
-
 par Paulrubens » 02 Oct 2016, 11:35
par Paulrubens » 02 Oct 2016, 11:35
quelqu'un?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 02 Oct 2016, 11:44
par XENSECP » 02 Oct 2016, 11:44
Paulrubens a écrit:quelqu'un?
c'est pas ce que j'appelle un résumé.
P: x²-4x+3
D: ax-6
intersection: x²-4x+3 = ax-6
soit: x² - (4+a)x + 9 = 0
soit un delta:
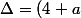^2 - 4 \times 9 = a^2 + 8a + 16 - 36 = a^2 + 8a - 20)
CQFD
-
Paulrubens
- Membre Naturel
- Messages: 20
- Enregistré le: 01 Oct 2016, 18:32
-
 par Paulrubens » 02 Oct 2016, 11:54
par Paulrubens » 02 Oct 2016, 11:54
XENSECP a écrit: Paulrubens a écrit:quelqu'un?
c'est pas ce que j'appelle un résumé.
P: x²-4x+3
D: ax-6
intersection: x²-4x+3 = ax-6
soit: x² - (4+a)x + 9 = 0
soit un delta:
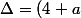^2 - 4 \times 9 = a^2 + 8a + 16 - 36 = a^2 + 8a - 20)
CQFD
d'accord merci de votre aide
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 02 Oct 2016, 12:00
par XENSECP » 02 Oct 2016, 12:00
Paulrubens a écrit: XENSECP a écrit: Paulrubens a écrit:quelqu'un?
c'est pas ce que j'appelle un résumé.
P: x²-4x+3
D: ax-6
intersection: x²-4x+3 = ax-6
soit: x² - (4+a)x + 9 = 0
soit un delta:
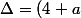^2 - 4 \times 9 = a^2 + 8a + 16 - 36 = a^2 + 8a - 20)
CQFD
d'accord merci de votre aide
Tu noteras que j'ai "juste" repris les infos du topic et conclus

-
Paulrubens
- Membre Naturel
- Messages: 20
- Enregistré le: 01 Oct 2016, 18:32
-
 par Paulrubens » 02 Oct 2016, 12:05
par Paulrubens » 02 Oct 2016, 12:05
oui je vois ça j'ai peut être manqué de jugeote pour le coup

-
Paulrubens
- Membre Naturel
- Messages: 20
- Enregistré le: 01 Oct 2016, 18:32
-
 par Paulrubens » 02 Oct 2016, 13:30
par Paulrubens » 02 Oct 2016, 13:30
Mais du coup, pour la question 6, c'est quoi une tangente de P passant par A?
-
Dasson2
- Membre Relatif
- Messages: 152
- Enregistré le: 24 Sep 2016, 17:00
-
 par Dasson2 » 02 Oct 2016, 16:12
par Dasson2 » 02 Oct 2016, 16:12
Les abscisses des points d'intersection de la droite "y=ax-6" et de la parabole "y=x²-4x+3" sont solution de
x²-(a+4)x+9=0 (E)
Etudier le signe de delta=a²+8a-20
Si delta<0, c'est à dire si a<-10 ou bien a>2 alors (E) n'a pas de solution : la droite et la parabole n'ont pas de point commun.
Si delta>0, c'est à dire si -10<a<2 alors (E) a deux solutions : la droite et la parabole ont deux points communs.
Si delta =0 c'est à dire si a=-10 ou a=2 alors (E) a une solution double : la droite et la parabole ont un seul point commun, ce qui correspond aux tangentes d'équations y=-10x-6 et y=2x-6 (droite (AB)).
A suivre sur mon tit programme. Mais il ne fonctionne peut-être pas ????
-
Paulrubens
- Membre Naturel
- Messages: 20
- Enregistré le: 01 Oct 2016, 18:32
-
 par Paulrubens » 02 Oct 2016, 20:25
par Paulrubens » 02 Oct 2016, 20:25
Dasson2 a écrit:Les abscisses des points d'intersection de la droite "y=ax-6" et de la parabole "y=x²-4x+3" sont solution de
x²-(a+4)x+9=0 (E)
Etudier le signe de delta=a²+8a-20
Si delta<0, c'est à dire si a<-10 ou bien a>2 alors (E) n'a pas de solution : la droite et la parabole n'ont pas de point commun.
Si delta>0, c'est à dire si -10<a<2 alors (E) a deux solutions : la droite et la parabole ont deux points communs.
Si delta =0 c'est à dire si a=-10 ou a=2 alors (E) a une solution double : la droite et la parabole ont un seul point commun, ce qui correspond aux tangentes d'équations y=-10x-6 et y=2x-6 (droite (AB)).
A suivre sur mon tit programme. Mais il ne fonctionne peut-être pas ????
donc si je vous suis, vous avez utilisé delta de a²+8a-20 afin de trouver -10 et 2 pour solutions de a, les solutions étants -10x-6 et 2x-6. Donc pour répondre à ma question je dois tracer ces deux droites sur ma copie en plus de la parabole pour montrer les tangentes de P par la point A c'est juste?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
CQFD
CQFD