Bonjour et veuillez pardonner la longueur du message,
Dans un livre j'ai lu la définition suivante de

:
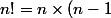 \times \cdots \times \frac{n}{2} \times (\frac{n}{2}-1) \times \cdots \times 2 \times 1)
(définition introduite pour permettre de minorer

, voir la fin du message)
J'ai du mal à comprendre la partie
 \times \cdots)
de cette définition.
Cas n pair : (pas de problème)
En effet, si

est pair je n'ai pas de problème, par exemple si
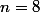
, alors

et
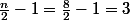
et on a bien
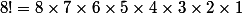
.
Cas n impair : (problème)
Mais si

est impair, par exemple si
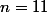
que faire de
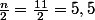
et de
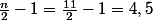
. Injectés dans la définition cela donnerait quelque chose comme
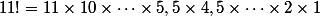
ce qui pour moi n'a aucun sens.
Cette définition implique-t-elle qu'il faille choisir d'éliminer un des facteur
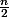
ou
)
en fonction de la parité de

? Si c'est le cas, comment le deviner à la seule lecture de cette définition ? Bref, je ne comprends pas comment interpréter cette définition.
Ma première question : pourriez-vous m'aider à interpréter cette définition ? Et ce quelle que soit la parité de

-------------------------------
La minoration en question :
Et, pendant que j'y suis, comment fait l'auteur pour trouver qu'il y a
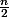
facteurs
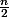
dans la ligne 2, c'est-à-dire comment fait-il pour trouver
}^{n/2})
. Car, en ce qui me concerne, dans la ligne 1, de

à
)
inclus, il y a
)
facteurs, donc pour trouver le nombre de
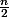
dans la ligne 2 il suffit de faire
)
, autrement dit, de

à
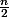
inclus, n'y a-t-il pas de
=\frac{n}{2}+1)
facteurs
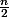
car :
 &=& n-\frac{n}{2}+1\\<br />&=& \frac{2n-n+2}{2}\\<br />&=& \frac{n+2}{2}\\<br />&=& \frac{n}{2}+1<br />\end{array})
Ligne 2, ne devrions nous pas avoir plutot :
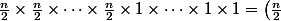}^{(n/2)+1})
Ma deuxième question : pourriez-vous m'aider à déterminer le nombre de facteur
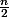
dans la ligne 2, c'est-à-dire la puissance à laquelle élever
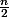
dans la ligne 2 ? Devrait-on avoir
}^{(n/2)+1})
ou
}^{n/2})
et pourquoi ?
Merci.
