Par exemple :
Définir le domaine d'un système
5 messages
- Page 1 sur 1
définir le domaine d'un système
bonjour, j'aimerais savoir comment définir le domaine de définition d'un système de deux équations à deux inconnues.
Par exemple :
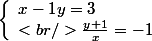 , ici,
, ici, 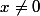 et
et 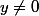 , mais comment définir le domaine à partir de ça ?
, mais comment définir le domaine à partir de ça ?
Par exemple :
Dinozzo13 a écrit:bonjour, j'aimerais savoir comment définir le domaine de définition d'un système de deux équations à deux inconnues.
Par exemple :, ici,
et
, mais comment définir le domaine à partir de ça ?
Deux équations, deux variables. Tu cherches des solutions réels. Donc les solutions réelles sont à chercher dans
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
