Bonsoir,
Voici un nouveau défi que nous lance notre prof et affirme que personne ne parviendra à le relever. Une semaine que je cherche et rien.
Qu'en pensez-vous ?
f est une fonction numérique définie sur [0;1]
et f(1) < 0 < f(0)
On suppose qu'il existe une fonction numérique g continue sur [0;1] tel que f + g est croissante .
Montrez que f(D) = 0 tel qu'il existe un D appartenant à [0 ;1]
N.B : ( Attention f n'est pas continue sur [0;1] ) Donc, on ne doit pas appliquer le théorème des valeurs intermédiaires.
Merci d'essayer.
Défi
3 messages
- Page 1 sur 1
Salut,
Perso, je chercherais un D tel que f(D)=0 en procédant par dichotomie, c'est à dire en considérant les deux suites_{n\geq 0}) et
et _{n\geq 0}) définies par :
définies par :
0\text{ alors }<br />\left\{\matrix{U_{n+1}=\frac{U_n+V_n}{2}\cr V_{n+1}=V_n\ \ \ \ \ \ }\right.\ \text{ sinon }<br />\left\{\matrix{U_{n+1}=U_n\ \ \ \ \ \ \cr V_{n+1}=\frac{U_n+V_n}{2} }\right.)
On montre aisément (archi classique) que_{n\geq 0}) est croissante,
est croissante, _{n\geq 0}) décroissante, qu'elles convergent vers une limite commune
décroissante, qu'elles convergent vers une limite commune 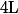 , et que, pour tout
, et que, pour tout 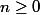 ,
, \leq 0 < f(U_n)\ (#))
Il faut maintenant utiliser l'hypothèse disant que s'écrit sous la forme
s'écrit sous la forme 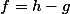 avec
avec  croissante et
croissante et 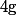 continue :
continue :
- Comme est croissante, la suite
est croissante, la suite \big)_{n\geq 0}) est croissante et majorée par
est croissante et majorée par ) donc converge vers une limite
donc converge vers une limite ) .
.
- Comme est croissante, la suite
est croissante, la suite \big)_{n\geq 0}) est décroissante et minorée par
est décroissante et minorée par ) donc converge vers une limite
donc converge vers une limite ) .
.
- Comme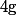 est continue, les deux suites
est continue, les deux suites \big)_{n\geq 0}) et
et \big)_{n\geq 0}) convergent toute les deux vers
convergent toute les deux vers ) (vu en terminale ???)
(vu en terminale ???)
En faisant tendre vers l'infini dans l'inégalité
vers l'infini dans l'inégalité 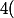) , on a donc
, on a donc \leq 0\leq A-g(L)\) .
.
Mais on a aussi\leq h(L)-g(L) \leq B-g(L)) donc en fait
donc en fait -g(L)=0) , c'est à dire
, c'est à dire =0) .
.
Perso, je chercherais un D tel que f(D)=0 en procédant par dichotomie, c'est à dire en considérant les deux suites
On montre aisément (archi classique) que
Il faut maintenant utiliser l'hypothèse disant que
- Comme
- Comme
- Comme
En faisant tendre
Mais on a aussi
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
WAW bien vu . Merci.
Merci infiniment , je crois que c'est bien démontré.
Ben314 a écrit:Salut,
Perso, je chercherais un D tel que f(D)=0 en procédant par dichotomie, c'est à dire en considérant les deux suiteset
définies par :
On montre aisément (archi classique) queest croissante,
décroissante, qu'elles convergent vers une limite commune
, et que, pour tout
,
Il faut maintenant utiliser l'hypothèse disant ques'écrit sous la forme
avec
croissante et
continue :
- Commeest croissante, la suite
est croissante et majorée par
donc converge vers une limite
.
- Commeest croissante, la suite
est décroissante et minorée par
donc converge vers une limite
.
- Commeest continue, les deux suites
et
convergent toute les deux vers
(vu en terminale ???)
En faisant tendrevers l'infini dans l'inégalité
, on a donc
.
Mais on a aussidonc en fait
, c'est à dire
.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
