Défi limite d'une suite et fonction continue

[Henri_Golo]

Soit (Vn) la suite définie sur N’ par : Vn =E(1 ). Comment, en se servant de cette suite démontrer que sans l’hypothèse de continuité, le théorème de limite d'une suite et fonction continue, a savoir :
n'est pas valide.

[Imod]

Soit (Vn) la suite définie sur N’ par : Vn =E(1 ). Comment, en se servant de cette suite démontrer que sans l’hypothèse de continuité, le théorème de limite d'une suite et fonction continue, a savoir :
n'est pas valide.

Tu es sûr de ta suite , pour moi !

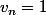
Imod

[Henri_Golo]

Oui oui, je suis bien sur de la suite,
V(n)=E(1-(1/n)) , ou E est la partie entière, et Vn n'est pas égal a 1 puisque la suite varie en fonction de n.

[chan79]

eh oui
1-1/n tend vers 1
mais dès que n>1, on a 0<1-1/n<1 donc E(1-1/n)=0 sa limite est 0 et non pas E(1) qui est égal à 1.
ce qui ne met pas en défaut la propriété énoncée puisque E n'est pas continue

[Imod]

D'accord vu comme ça . Le -1/n ayant pris un peu de hauteur j'avais cru que c'était un exposant :marteau:

Imod