capitaine nuggets a écrit:Après, un truc qui peut t'être utile, c'est de savoir ce que tu as vu en cours : si tu as vu des histoires de triangles avec Pythagore et qu'on te donne des exos dessus, il y a gros à parier qu'on va devoir prendre des triangles auxquels on appliquera le théorème ou sa réciproque :lol3:
C'est sûr qu'après une bonne nuit de sommeil on voit les choses plus clairement :dodo:
Bonne nuit à toi :we:
Bonjour,
Après une nuit agitée où je n'ai rêvé que de cet exercice, je me suis réveillée tôt ce matin avec quelques idées en tête. J'ai essayé de les appliquer mais je bloque toujours.
En suivant ton conseil, je voulais démontrer que dans le plan ABIH, le triangle AMH (ou ABM) est rectangle en M. Seulement, je ne sais pas comment calculer BH en fonction de a pour avoir MH (ou BM).
Je sais que BM=1/3 BH d'après la 2e question.
Ci-joint mes réponses à cet exercice jusqu'au 3)a).
http://www.fichier-pdf.fr/2015/01/13/geometrie/Peux-tu me dire si ce que j'ai fait est juste?
Parce que si c'est faux, je comprends pourquoi je n'arrive pas à faire le 3)b), sinon, peux-tu m'aiguiller un peu plus pour cette dernière question?
A priori, je dois trouver BH=
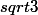
a (car si le triangle ABM est rectangle en M, d'après l'égalité de Pythagore: AB² = AM²+MB², sachant que AB=a, AM = 2/3 AI et
AI =

a, on trouve MB =

a et comme BH = 3MB alors BH=
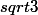
a)
Seulement, on doit démontrer que ABM est rectangle???

