Cube
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
faalw
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Sep 2013, 14:00
-
 par faalw » 22 Sep 2013, 09:55
par faalw » 22 Sep 2013, 09:55
Bonjour a tous,
je suis actuellement bloqué sur un de mes exercices de mathématiques:
Si on augmente la longueur de l'arête d'un cube, son volume augmente alors de 2 403cm cube.
Combien mesure l'arête de ce cube?
Quelqu'un peut me mettre sur la piste?
Merci!
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 22 Sep 2013, 09:58
par XENSECP » 22 Sep 2013, 09:58
Si on augmente de combien?
-
faalw
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Sep 2013, 14:00
-
 par faalw » 22 Sep 2013, 09:59
par faalw » 22 Sep 2013, 09:59
XENSECP a écrit:Si on augmente de combien?
Oups! On augmente de 2cm
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 22 Sep 2013, 10:01
par XENSECP » 22 Sep 2013, 10:01
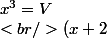^3 = V + 2403)
Petit système (mais en fait V on s'en fiche) donc petite équation à résoudre

-
faalw
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Sep 2013, 14:00
-
 par faalw » 22 Sep 2013, 10:04
par faalw » 22 Sep 2013, 10:04
XENSECP a écrit: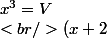^3 = V + 2403)
Petit système (mais en fait V on s'en fiche) donc petite équation à résoudre

Donc V= (x+2)^3-2402
Et la?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 22 Sep 2013, 10:06
par XENSECP » 22 Sep 2013, 10:06
Il faut éliminer V ...
-
faalw
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Sep 2013, 14:00
-
 par faalw » 22 Sep 2013, 10:10
par faalw » 22 Sep 2013, 10:10
XENSECP a écrit:Il faut éliminer V ...
Donc V= (x+2)^3-2402
0= [(x+2)^3-2402]/v
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 22 Sep 2013, 10:12
par XENSECP » 22 Sep 2013, 10:12
faalw a écrit:Donc V= (x+2)^3-2402
0= [(x+2)^3-2402]/v
Il faut utiliser les 2 équations.
Bon si tu n'y mets pas du tien, je vais arrêter d'essayer de t'aider.
-
faalw
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Sep 2013, 14:00
-
 par faalw » 22 Sep 2013, 10:16
par faalw » 22 Sep 2013, 10:16
XENSECP a écrit:Il faut utiliser les 2 équations.
Bon si tu n'y mets pas du tien, je vais arrêter d'essayer de t'aider.
Je crois que je viens de comprendre:
Donc V= (x+2)^3-2402
x^3=(x+2)^3-2402
0=(x+2)^3-2402-x^3
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 22 Sep 2013, 10:34
par XENSECP » 22 Sep 2013, 10:34
Oui!
Maintenant tu développes (x+2)^3 et simplifie l'équation :)
-
faalw
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Sep 2013, 14:00
-
 par faalw » 22 Sep 2013, 10:44
par faalw » 22 Sep 2013, 10:44
Je ne suis pas sur mais je vais essayé:
(x+2)^3 = (x+2)(x+2)²
= (x+2)(x²+4x+4)
= x^3+4x²+4x+2x²+8x+8
= x^3+6x²+12x+8
Je remplace dans l'équation:
0= x^3+6x²+12x+8-2402-x^3
0=6x²+12x-2394
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 22 Sep 2013, 10:45
par XENSECP » 22 Sep 2013, 10:45
Simplifie et résous :)
-
faalw
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Sep 2013, 14:00
-
 par faalw » 22 Sep 2013, 10:52
par faalw » 22 Sep 2013, 10:52
Alors
0=6(x²+2x-399)
Soit 6=0 ou x²+2x-399=0
soit 6=0 ou x²+2x=399
Après je bloque avec le carré..
-
triumph59
- Membre Rationnel
- Messages: 643
- Enregistré le: 16 Mar 2013, 16:49
-
 par triumph59 » 22 Sep 2013, 11:04
par triumph59 » 22 Sep 2013, 11:04
faalw a écrit:Alors
0=6(x²+2x-399)
Soit 6=0 ou x²+2x-399=0
soit 6=0 ou x²+2x=399
Après je bloque avec le carré..
Juste une question, dans l'énoncé ton volume augmente de

et ensuite tu utilises 2402, quelle est la bonne valeur ?
-
faalw
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Sep 2013, 14:00
-
 par faalw » 22 Sep 2013, 11:08
par faalw » 22 Sep 2013, 11:08
Ouap! Faute de frappe! Le volume augmente de 2402cm^3
Désolé :-)
-
triumph59
- Membre Rationnel
- Messages: 643
- Enregistré le: 16 Mar 2013, 16:49
-
 par triumph59 » 22 Sep 2013, 11:17
par triumph59 » 22 Sep 2013, 11:17
faalw a écrit:Ouap! Faute de frappe! Le volume augmente de 2402cm^3
Désolé

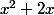
ça ressemble presque à une identité remarquable, si tu as
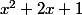
ça te fait penser à quoi ?
-
faalw
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Sep 2013, 14:00
-
 par faalw » 22 Sep 2013, 11:20
par faalw » 22 Sep 2013, 11:20
x²+2x=399
(x+1)²-1=399
(x+1)²=400
x+1=racine de 400
x=20-1
x=19
-
triumph59
- Membre Rationnel
- Messages: 643
- Enregistré le: 16 Mar 2013, 16:49
-
 par triumph59 » 22 Sep 2013, 11:41
par triumph59 » 22 Sep 2013, 11:41
faalw a écrit:x²+2x=399
(x+1)²-1=399
(x+1)²=400
x+1=racine de 400
x=20-1
x=19
La 2ème solution possible est

x=-21 qui ne convient pas car l'arête du cube doit être un nombre positif
Donc ok pour ta réponse :we:
Tu peux aussi transformer
^2=400)
en
^2-20^2=0)
ce qui donne
(x+1-20)=0)
... plus "pro" comme façon de résoudre :id:
-
faalw
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Sep 2013, 14:00
-
 par faalw » 22 Sep 2013, 11:45
par faalw » 22 Sep 2013, 11:45
Ok parfait!
Merci beaucoup :-)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
