Croissance d'une fonction

par **Le_chat** » 03 Sep 2009, 16:09

Salut a toutes et a tous.
J'ai un petit exercice:
Soit

avec x dans R+*
Il s'agit de prouver que cette fonction est croissante.
J'ai ainsi calculé

Jusque la c'est bon?
ensuite cela se corse, je n'arrive pas a conclure sur la positivité de f'(x).
Quelqu'un pourrait m'indiquer une piste?

par **le_fabien** » 03 Sep 2009, 16:34

Bonjour,
peut être en calculant la dérivée seconde .

par **Sve@r** » 03 Sep 2009, 16:35

C'est vieux mais il me semble qu'il y a un truc avec

Or, en posant

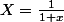
puis en regardant l'équation ln(X)=X, tu arrives à

par **le_fabien** » 03 Sep 2009, 16:38

J'ai fait les calculs , avec la dérivée seconde on y arrive , cool !

par **Le_chat** » 03 Sep 2009, 17:58

Merci pour ces reponses!
J'ai calculé la derivée seconde

c'est bon?

Il faut que je calcule la limite en+ l'infini de f'(x)?? parceque je retombe sur une forme indeterminée

EDIT: ah bah non :stupid_in je croyais que 0-0 etait une FI.

Merci beaucoup a vous deux, bonne soirée :++:

par **le_fabien** » 03 Sep 2009, 18:41

Le_chat a écrit:Merci pour ces reponses!
J'ai calculé la derivée seconde
c'est bon?

Il faut que je calcule la limite en+ l'infini de f'(x)?? parceque je retombe sur une forme indeterminée

EDIT: ah bah non :stupid_in je croyais que 0-0 etait une FI.

Merci beaucoup a vous deux, bonne soirée :++:

Et oui tu as donc f'(x) toujours positive.

Croissance d'une fonction

Croissance d'une fonction

Qui est en ligne