Croissance par récurrence

[Lechero]

[...]

On a : Up

On multiplie par 9

>

On additionne Up

Up + > + Up

On multiplie par 1/2

> \frac{9}{\frac{1}{2^p} + 3}[/TEX] + Up)

> + Up)

Je crois que ca sert à rien ce que je viens de faire ...

[Mortelune]

On dirait oui, tu as essayé de montrer l'intermédiaire proposé par Ben hier soir ?

[Lechero]

Non car comme je l'ai dit, je n'ai rien compris à ce qu'il a fait ... Désolé ^^

[Mortelune]

Salut,
Ben l'initialisation est (comme toujours) trés façile :
Est il vrai que ?

Ensuite, pour l'hérédité, vu que la suite est géométrique de raison , je te suggérerais bien de commencer par montrer (sans récurrence...) que, pour tout n dans N, ...

En fait si tu regardes ce que tu veux démontrer et ton hypothèse de récurrence on peut remarquer qu'en faisant une division (tous les termes sont strictement positifs donc ça ne pose pas de problème) on retombe sur ce qu'il te propose de démontrer, ce qui revient à démontrer l'hérédité comme ça représente à peu près tout le travail (et ça se fait très bien) ^^

[Lechero]

Je dois prouver que Un - 3 < .


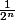
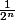
Je ne vois pas d'où sort le ()n, ni à quoi ca sert de savoir qu'elle est géométrique, etc...

Je vois vraiment pas où est le rapport, c'est ca qui me bloque ...

[bentaarito]

es tu d'accord que si tu montres que
on gagne car par hypothèse de récurrence on a : ??

[Mortelune]

Si elle est géométrique ça veut dire que pour passer au rang suivant il faut multiplier par 1/2.

Et le puissance n c'est pour l'hérédité, ça vient de ton énoncé.

Donc si tu arrives à montrer ce qu'il propose et que tu multiplie tout par Un-3(>0), ton hypothèse de récurrence te donnera la solution.

[Lechero]

)


Pfffiou ça m'énerve ! C'est moi qui est un problème ou c'est vraiment chiant ? ^^

[Mortelune]

C'est toi

Tu y vas dans le désordre, tu devrais savoir qu'un dénominateur c'est pas pratique :

[Lechero]

=)

J'étais arrivé jusque là, mais sans comprendre pourquoi en fait...

je remplace par sa valeur ?

Dois-je avant tout démontrer qu'elle a pour raison q= 1/2 ?

[nodjim]

Je ne comprends pas pourquoi on ne fait jamais utiliser cette petite astuce bien pratique pour les suites:
On dessine sur graphe la fonction y=f(x) et y=x.
Sur le même graphe, on échange l'axe des x avec l'axe des y et on redessine y=f(x).
Les solutions de la suite apparaissent alors presque immédiatement, en faisant se balader d'une courbe à l'autre une valeur initiale.

[Mortelune]

Non tu ne remplaces rien tu majores le terme de droite de l'inégalité avec ton hypothèse de récurrence (une fois que tu as démontré l'inégalité de Ben).

[Lechero]

Je ne vois pas comment le démontrer ... :







Je sais pas si c'est ça, si c'est utile, ... La puissance n me bloque totalement et me fait peur, je ne comprends rien de rien. L'inégalité de Ben je ne sais même pas d'où elle sort, ça me parait trop compliqué ...

[Mortelune]

(l'initialisation est faite)

Tu as ton hypothèse de récurrence :
Tu veux démontrer :

Donc si tu sais que tu vas pouvoir écrire que :

[Lechero]

(l'initialisation est faite)

Tu as ton hypothèse de récurrence : ==> OK
Tu veux démontrer : ==> OK

Donc si tu sais que tu vas pouvoir écrire que :

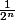
Voilà ce qui me "perturbe". est géom de raison q=1/2, ça je viens de le faire au brouillon .

Mais je ne vois pas où est le rapport, je ne vois vraiment vraiment pas, je suis désolé de ne rien comprendre là ...

[Mortelune]

Tu n'as pas à ne pas être d'accord avec le "si tu sais que" puisque c'est son utilité que je veux te justifier :P

La suite géométrique n'a rien d'essentielle dans la démonstration si tu comprends le reste.

[Lechero]

Justement, son utilité bah... Je ne vois pas en quoi ca peut nous aider (ne me tape pas =p )

[Mortelune]

ça permet de passer à la dernière ligne qui justifie donc l'hérédité mais à part ça ça sert à rien c'est vrai :P

[Lechero]

Ah !! Je crois avoir compris !

Dis moi juste comment tu arrives à ca et je pense avoir compris !

Merciiiiiiiii !!

[Mortelune]

En multipliant les 2 termes de ton hypothèse de récurrence par 1/2.