Croissance par récurrence
71 messages
- Page 2 sur 4 - 1, 2, 3, 4
Ok donc reprenons.
Tu as une suite définie par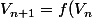)
Si sur un graphique tu traces les droites d'équation y=x et y=f(x) tu observes qu'il y a 1 point d'intersection.
Tu as du voir une méthode pour trouver les éléments successifs de la suite grâce à ce graphique en ayant et les 2 droites d'équation données avant.
et les 2 droites d'équation données avant.
On observe que la suite tend vers un point et c'est l'ordonnée de ce point que l'on cherche.
On voit que si on applique à ce point une itération de l' "algorithme" utilisé avant pour avoir quelques éléments successifs de la suite on aura en image ce même point.
Ce qui se traduit par l'égalité que je t'ai donné avant :
On se ramène à une équation du second degré en l à résoudre.
Tu as une suite définie par
Si sur un graphique tu traces les droites d'équation y=x et y=f(x) tu observes qu'il y a 1 point d'intersection.
Tu as du voir une méthode pour trouver les éléments successifs de la suite grâce à ce graphique en ayant
On observe que la suite tend vers un point et c'est l'ordonnée de ce point que l'on cherche.
On voit que si on applique à ce point une itération de l' "algorithme" utilisé avant pour avoir quelques éléments successifs de la suite on aura en image ce même point.
Ce qui se traduit par l'égalité que je t'ai donné avant :
On se ramène à une équation du second degré en l à résoudre.
Non mais c'est bon, j'ai trouvé finalement ! =) Merci !
Mais voilà une autre question ^^ :
Je dois démontrer par récurrence que 3 minore une suite Un, avec Uo=4 et Un+1 =)
Initialisation : Uo = 4 et 4>3 la propriété est vérifiée au rang 0
Hérédité: Soit p appartient à N un rand fiwé tel que la propriété est vraie, soit Up > 3
Montrons [...] soit Up+1 > 3
On a Up > 3
 <
<  (on a appliqué la fonction inverse qui est décroissante)
(on a appliqué la fonction inverse qui est décroissante)
 <
< 
 < 3
< 3
Up + < 3 + Up
< 3 + Up
 (Up +
(Up +  ) <
) <  (3+Up)
(3+Up)
Up+1 < (3+Up)
(3+Up)
Mais ça ne démontre pas que 3 minore Up+1, j'ai du faire une erreur mais je la vois pas du tout ...
Mais voilà une autre question ^^ :
Je dois démontrer par récurrence que 3 minore une suite Un, avec Uo=4 et Un+1 =
Initialisation : Uo = 4 et 4>3 la propriété est vérifiée au rang 0
Hérédité: Soit p appartient à N un rand fiwé tel que la propriété est vraie, soit Up > 3
Montrons [...] soit Up+1 > 3
On a Up > 3
Up +
Up+1 <
Mais ça ne démontre pas que 3 minore Up+1, j'ai du faire une erreur mais je la vois pas du tout ...
Tu n'as pas fait d'erreur, c'est juste que tu ne démontre pas ce qu'il faut ^^
Par contre on a :
 \geq 3 \Longleftrightarrow u_p^2+9 \geq 6u_p \Longleftrightarrow u_p^2-6u_p+9 \geq 0)
Donc démontrer ton hérédité revient à trouver les racines du polynôme en (puisqu'on a l'hypothèse de récurrence qui affirme qu'il est supérieur à 3) ce que tu dois savoir faire (et ça marche je l'ai fait
(puisqu'on a l'hypothèse de récurrence qui affirme qu'il est supérieur à 3) ce que tu dois savoir faire (et ça marche je l'ai fait  ).
).
Par contre on a :
Donc démontrer ton hérédité revient à trouver les racines du polynôme en
Up+1 > 3 on l'a dans l'hypothèse au rang p+1, nul part ailleurs...
Sinon j'ai compris, car le discriminant vaut 0, la solution vaut 4 donc Up+1 > 3
Mais comme je l'ai dit, Up+1 est uniquement dans l'hypothèse, donc je ne sais pas si on peut l'utiliser ...
Ce que tu as marqué, où-dois l'écrire par exemple ?
Sinon j'ai compris, car le discriminant vaut 0, la solution vaut 4 donc Up+1 > 3
Mais comme je l'ai dit, Up+1 est uniquement dans l'hypothèse, donc je ne sais pas si on peut l'utiliser ...
Ce que tu as marqué, où-dois l'écrire par exemple ?
Ah d'accord ! Donc dans l'hérédité, [...]
On a : Up > 3
Supposons que Up+1 > 3 (=) [...] (=) Up²-6Up+9 toujours positif, et donc que 3 minore Un.
On montre ainsi, bla bla bla ...
Merci beaucoup !
Est-ce la même chose si n > 3 ? Je dois d'abord démontrer avec n > 3 et après dire que c'est pour tout n de N...
On a : Up > 3
Supposons que Up+1 > 3 (=) [...] (=) Up²-6Up+9 toujours positif, et donc que 3 minore Un.
On montre ainsi, bla bla bla ...
Merci beaucoup !
Est-ce la même chose si n > 3 ? Je dois d'abord démontrer avec n > 3 et après dire que c'est pour tout n de N...
Salut,
Ben l'initialisation est (comme toujours) trés façile :
Est il vrai que ?
?
Ensuite, pour l'hérédité, vu que la suite_{n\geq 1}) est géométrique de raison
est géométrique de raison  , je te suggérerais bien de commencer par montrer (sans récurrence...) que, pour tout n dans N,
, je te suggérerais bien de commencer par montrer (sans récurrence...) que, pour tout n dans N,  ...
...
Ben l'initialisation est (comme toujours) trés façile :
Est il vrai que
Ensuite, pour l'hérédité, vu que la suite
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Le petit problème, pour l'initialisation, c'est que tu nous a donné un énoncé qui ne veut rien dire :
"montrer, par récurrence bien sûr, que, pour tout , on a Un - 3 <
, on a Un - 3 < 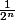 "
"
ce qui fait que j'ai fait l'amorce avec n=1.
P.S. Je pense que pour comprendre les maths, un premier truc, c'est de comprendre le sens de ce qu'on écrit et donc d'écrire des choses qui ont du sens.
Si quelqu'un dans la rue te dit juste "gris" est ce que ça coule de source que, ce qu'il a voulu dire c'est "tout les chats sont gris" ?
J'ai supposé que "le vrai" énoncé était :Lechero a écrit:Comment montrer, par récurrence bien sûr, que Un - 3 <?
"montrer, par récurrence bien sûr, que, pour tout
ce qui fait que j'ai fait l'amorce avec n=1.
P.S. Je pense que pour comprendre les maths, un premier truc, c'est de comprendre le sens de ce qu'on écrit et donc d'écrire des choses qui ont du sens.
Si quelqu'un dans la rue te dit juste "gris" est ce que ça coule de source que, ce qu'il a voulu dire c'est "tout les chats sont gris" ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Donc :
Montrons par récurrence que pour tout n 1, Un - 3 <
1, Un - 3 < 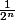
Initialisation : U1 = 3.125 et U1 - 3 <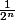 (=) 0.125 < 0.5 La propriété est vérifiée au rang 1
(=) 0.125 < 0.5 La propriété est vérifiée au rang 1
Hérédité : Soit p un entier naturel un rang fixé tel que la propriété est vraie, soit Up - 3 <
un rang fixé tel que la propriété est vraie, soit Up - 3 < 
Montrons qu'alors la propriété est vraie au rang p+1, soit Up+1 - 3 <
On a : Up - 3 <
et là comment je fais pour passer de p à p+1 ? ... (auparavant, j'ai étudié la fonction f(x) =)
Montrons par récurrence que pour tout n
Initialisation : U1 = 3.125 et U1 - 3 <
Hérédité : Soit p un entier naturel
Montrons qu'alors la propriété est vraie au rang p+1, soit Up+1 - 3 <
On a : Up - 3 <
et là comment je fais pour passer de p à p+1 ? ... (auparavant, j'ai étudié la fonction f(x) =
71 messages
- Page 2 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
