Cos(a+b) et sin(a+b)

[bengao]

Bonjour à tous.

Je cherche à résoudre


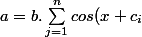l'inconnue est x que je souhaite trouver.

Est ce que quelqu'un aurait une idée ??

J'ai la même question mais avec sinus au lieu de cosinus

Merci de votre aide.

[siger]

bonjour
une idée : a voir?

en developpant les cosinus on a
cos(x+ci) = cosx cos(ci) + sinx sin(ci)
d'ou
a = b (A cosx + B sinx)
avec A= somme cos(ci) et B = somme sin (ci)

de meme en considerant sin(x+ci) on obtient
a' = b' (A sinx + B cosx)

.........

[bengao]

Merci Siger, j'y ai bien pensé, mais après....

[pascal16]

ce qu'il faut comprendre, c'est les ci sont des constantes, et que donc, la somme des n terme peut se simplifier en 1 seul qu'on peut 'facilement' résoudre si on est un pro de la trigo.

après tu tappes dans Google :
acosx+bsinx=c

et tu as la méthode générale.

[bengao]

merci pascal et siger, sympa , je regarde tout cela