pour une programmation , je suis a la recherche d'une solution pour trouver les coordonnées du 3eme point de mon triangle .. selon la figure suivante .
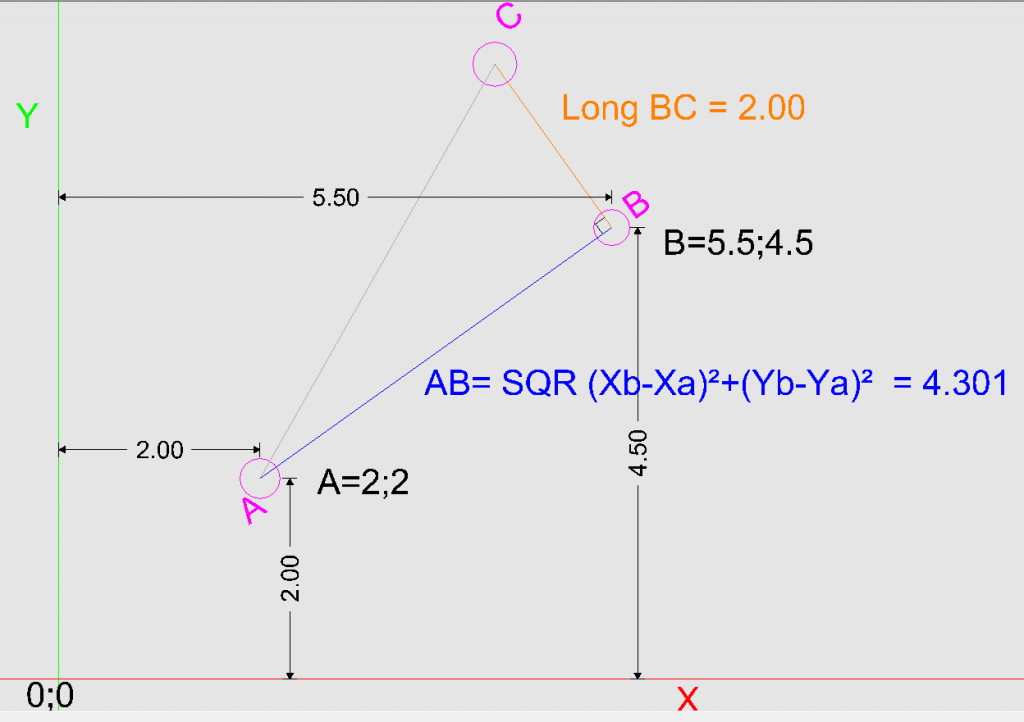
je connais les coordonnées de A et B
je sais que ABC forme un angle droit et que la longueur BC fait 2
j'arrive facilement a trouver la longueur de AB qui correspond a :
SQR(xb-xa)²+(yb-ya)² = 4.301
j'arrive donc facilement a trouver la longueur AC par Pythagore 4.7432
j'ai donc mes 3 longueurs ..mais je ne sais pas du tout comment trouver les coordonnées X et Y de C
j'ai réussi a posé les équation mais au final je me trouve toujours avec 2 inconnu :
AB = SQR( xb-xa)²+(yb-ya)²
BC = SQR(xc-xb)²+(yc-yb)²
AC = SQR(xc-xa)²+(yc-ya)²
(SQR pour la racine je ne sais pas comment écrire le symbole )
merci pour votre aide
