Convexité d'une fonction

[Juss]

bonjours ,

Voila mon exercice :

étudier la convexité de cette fonction , f(x) : ln(;)x)

' Convexité ' ???

Merci d'avance

[Dinozzo13]

Salut !
Je suppose que tu veux savoir ce que veut dire "convexe".
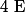
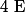
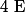
Ce que je sais, c'est qu'on dit qu'un ensemble de points du plan est convexe lorsque, pour tout couple de points de , le segment est inclus dans . Je pense donc que ça a un rapport avec, mais après je ne sais pas comment faire, désolé.

[benekire2]

en l'occurence si f''(x)>0 alors ta fonction est convexe.

[benekire2]

en fait f convexe signifie que f est au dessus de ces tangentes en tout points ( dans le cadre de fonctions différentiables)

[Dinozzo13]

Ouais donc j'étais carrément à côté de la plaque :ptdr:

[benekire2]

l'ennui c'est que ici

donc la fonction n'est pas convexe mais concave.

PS: J'ai mal lu l'énoncé c'était pas prouver la convexité mais étudier la convexité ( qui engloble la concavité)

[Dinozzo13]

Juste pour ma culture personnelle :ptdr: tu pourrais définir ce que tu entends par fonction concave ?

[Ben314]

Ouais donc j'étais carrément à côté de la plaque :ptdr:

PAS DU TOUT : une fonction est convexe lorsque l'ensemble des points situés au dessus de la courbe est convexe (avec ta def. de convexe pour un ensemble)
C'est pas complètement évident à démontrer, mais, si f est deux fois dérivable, cette propriété revient à dire que f''(x) est tout le temps positif ou nul.

[Ben314]

La question "étudier la convexité de f" ne veut pas dire "montrer qu'elle est convexe" mais "déterminer sur quels intervalles elle est convexe et sur lesquels elle est concave".
En résumé, cela veut dire qu'il faut étudier le signe de f''...

[Juss]

Alors si je comprend bien je calcule f ' ' (x)

[benekire2]

oui et comme ben l'a dit ensuite tuu étudie le signe de f'' et tu en déduit ( parce que je t'ai déjà calculé f'' ...) que ta fonction est tout le temps concave ( i.e pour dinozzo f''(x)>0 [contraire de la convexe] )

[Nightmare]

Il n'est d'ailleurs pas inintéressant pour un élève qui découvre la convexité de montrer qu'une fonction est convexe si et ssi son épigraphe l'est.