Convergence d'une suite: Aide pour l'encadrement

[SeifMaths]

Bonjour,



J'ai montré que W est croissante, mais je n'arrive pas à l'encadrer, avez-vous une idée pour le faire?

[Ben314]

Salut,
Je suis pas sûr que la monotonie de soit bien utile.
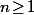
Par contre, vu le résultat de la question précédente, tu sait que pour tout tu as .
Donc . . .

[SeifMaths]

Salut,
Je suis pas sûr que la monotonie de soit bien utile.
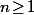
Par contre, vu le résultat de la question précédente, tu sait que pour tout tu as .
Donc . . .

Autrement dit, 1/n converge et g converge car -1/(1+n) converge donc Wn converge? Je ne suis pas encore convaincu

[Lostounet]

La quantité -1/(n+1) tend vers 0. Or la fonction g est dérivable sur R elle est donc continue en 0 la limite de g(-1/(n+1)) est donc g(0)

Et g(0)*-1/n tend vers 0 donc finalement vers quoi tend Wn?

[SeifMaths]

Bonjour,
Vu que l'on avait vu ce chapitre il y a longtemps, je ne me rappelle plus des détails.. Je me rappelle seulement qu'il fallait avoir la monotonie et l'encadrement d'une suite pour déterminer sa convergence, mais c'est clair maintenant
Je vous remercie les deux!

[Lostounet]

Une suite croissante et majorée est convergente c'est vrai mais ici nous avons une écriture explicite de la suite donc nous pouvons l'exploiter.