Convergence de suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 10:07
par Dante0 » 23 Oct 2011, 10:07
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 23 Oct 2011, 10:14
par nodjim » 23 Oct 2011, 10:14
Rien de rien ?
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 23 Oct 2011, 10:16
par SaintAmand » 23 Oct 2011, 10:16
Bonjour,
(Re)lis ton cours, les exemples et les exercices vus en cours et ensuite reviens avec un exemple ou un exercice que tu n'as pas compris.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 10:24
par Dante0 » 23 Oct 2011, 10:24
SaintAmand a écrit:Bonjour,
(Re)lis ton cours, les exemples et les exercices vus en cours et ensuite reviens avec un exemple ou un exercice que tu n'as pas compris.
C'est fait. Je reviens avec le même exercice.
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 23 Oct 2011, 10:32
par SaintAmand » 23 Oct 2011, 10:32
Dante0 a écrit:C'est fait. Je reviens avec le même exercice.
Cela veut tout dire... Tes exercices sont de simples applications du cours qui ne présentent aucune difficulté technique. Donc, à moins que tu ne sois un peu plus explicite sur tes difficultés, on ne peut que te faire l'exercice, ce qui n'a aucun intérêt, n'est-ce pas ?
Plus utile (et honnête) est de nous montrer un exemple ou un exercice fait en classe. Tu donnes la solution du prof en indiquant précisement ce que tu ne comprends pas.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 10:35
par Dante0 » 23 Oct 2011, 10:35
SaintAmand a écrit:Cela veut tout dire... Tes exercices sont de simples applications du cours qui ne présentent aucune difficulté technique. Donc, à moins que tu ne sois un peu plus explicite sur tes difficultés, on ne peut que te faire l'exercice, ce qui n'a aucun intérêt, n'est-ce pas ?
Plus utile (et honnête) est de nous montrer un exemple ou un exercice fait en classe. Tu donnes la solution du prof en indiquant précisement ce que tu ne comprends pas.
Tout à fait.
Pourtant ce sont les seules applications que je n'arrive pas à résoudre.
La limite de la 1ere est 0 mais comment le montrer ?
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 23 Oct 2011, 10:37
par SaintAmand » 23 Oct 2011, 10:37
Dante0 a écrit:Tout à fait.
Pourtant ce sont les seules applications que je n'arrive pas à résoudre.
La limite de la 1ere est 0 mais comment le montrer ?
Qu'est-ce qui te fait dire que la limite est 0 ?
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 10:41
par Dante0 » 23 Oct 2011, 10:41
SaintAmand a écrit:Qu'est-ce qui te fait dire que la limite est 0 ?
Ma calculatrice.
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 23 Oct 2011, 10:55
par SaintAmand » 23 Oct 2011, 10:55
Dante0 a écrit:Ma calculatrice.
Ok, à défaut de mieux...
En tout cas si tu n'es pas capable de dire ce qui te gêne dans ces exercices, c'est que tu n'as pas assimilé les exemples et exercices vus en cours comme tu le prétends.
Soit la suite
_{n\geq 1})
définie par
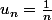
. Quelle est sa limite en +infini ?
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 11:07
par Dante0 » 23 Oct 2011, 11:07
SaintAmand a écrit:Ok, à défaut de mieux...
En tout cas si tu n'es pas capable de dire ce qui te gêne dans ces exercices, c'est que tu n'as pas assimilé les exemples et exercices vus en cours comme tu le prétends.
Soit la suite
_{n\geq 1})
définie par
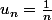
. Quelle est sa limite en +infini ?
0
Ok en gros ce qui me gêne , le -1 et l'exposant n , donc on va devoir distinguer 2 cas ou n est pair et ou il est impair.
Je vois ou tu veux me mener avec ton exemple :
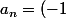^n.\frac{1}{n})
^n = -1)
si n est impair et
^n = 1)
si n est pair.
En multipliant par
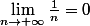
on obtient bien
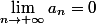
dans les 2 cas.
-
Bony
- Membre Relatif
- Messages: 123
- Enregistré le: 11 Oct 2011, 20:54
-
 par Bony » 23 Oct 2011, 11:12
par Bony » 23 Oct 2011, 11:12
Bon sang.
Comment tu peux dire si n est pair ou non à l'infini?
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 23 Oct 2011, 11:17
par SaintAmand » 23 Oct 2011, 11:17
Bony a écrit:Bon sang.
Comment tu peux dire si n est pair ou non à l'infini?
En plus c'est n qui tend vers l'infini, pas x. Dante0 est l'un de ces automaths dont Stella Baruk parle dans
l'Àge du capitaine.
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 23 Oct 2011, 11:28
par LeJeu » 23 Oct 2011, 11:28
Bonjour tout le monde,
J'ai lu aussi Stella Baruk, elle est plus compréhensive que vous ... vous pourriez donner un coup de main à Dante0 et ne pas être si moqueur et cassant ?
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 11:34
par Dante0 » 23 Oct 2011, 11:34
SaintAmand a écrit:En plus c'est n qui tend vers l'infini, pas x. Dante0 est l'un de ces automaths dont Stella Baruk parle dans l'Àge du capitaine.
Pardon pour l'erreur.
J'ai pas compris le message du dessus.
Merci LeJeu

-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 23 Oct 2011, 11:56
par LeJeu » 23 Oct 2011, 11:56
Bony a écrit:Bon sang.
Comment tu peux dire si n est pair ou non à l'infini?
Pourtant ca me semblait correct ? Mal dit mais pas complètement faux ?
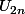
&
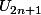
deux sous suites convergentes vers la même limite : ca peut être un chemin valable ? Non ?
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 23 Oct 2011, 11:56
par Billball » 23 Oct 2011, 11:56
aprés tu peux factoriser par le plus haut terme
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 23 Oct 2011, 11:58
par SaintAmand » 23 Oct 2011, 11:58
LeJeu a écrit:Bonjour tout le monde,
J'ai lu aussi Stella Baruk, elle est plus compréhensive que vous ... vous pourriez donner un coup de main à Dante0 et ne pas être si moqueur et cassant ?
Pour vous l'aider c'est faire son travail je suppose. Car je l'ai aidé. C'est bien suite à mes messages qu'il a fini par proposer quelque chose.
Quant au reste, cela frise le ridicule.
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 23 Oct 2011, 12:04
par SaintAmand » 23 Oct 2011, 12:04
LeJeu a écrit: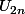
&
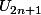
deux sous suites convergentes vers la même limite : ca peut être un chemin valable ? Non ?
Non, parce-que:
1) Dante0 est au lycée
2) il y a beaucoup plus élémentaire et simple
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 23 Oct 2011, 12:11
par LeJeu » 23 Oct 2011, 12:11
Ca me va ...
Donc on ne dit plus à Dante0 qu'il n"a pas le droit de considérer n pair & impair, mais qu'il y a plus simple ( et que son idée est intéressante mais non retenue....)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 12:37
par Dante0 » 23 Oct 2011, 12:37
SaintAmand a écrit:Pour vous l'aider c'est faire son travail je suppose. Car je l'ai aidé. C'est bien suite à mes messages qu'il a fini par proposer quelque chose.
Quant au reste, cela frise le ridicule.
...
Bon qu'est-ce qui est faux dans ce que j'ai mis ? Parce que si tout le monde propose une méthode différente on est pas sorti de l'auberge.
SaintAmand a écrit:Non, parce-que:
1) Dante0 est au lycée
2) il y a beaucoup plus élémentaire et simple
Je ne suis pas au lycée.
LeJeu a écrit:Ca me va ...
Donc on ne dit plus à Dante0 qu'il n"a pas le droit de considérer n pair & impair, mais qu'il y a plus simple ( et que son idée est intéressante mais non retenue....)
Quel esr le problème avec ma méthode ? Même au lycée on faisait ca.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
définie par
. Quelle est sa limite en +infini ?