Continuité d'une fonction

[yannvallet]

Bonjour,

Je doit étudier la continuité de la fonction suivante : (x+2)/(4x-1)

J'ai répondu le domaine de définition est R-{1/4}
La fonction est continu sur ]-oo, 1/4[ et sur ]1/4, +oo[
Est-ce que ma réponse est suffisante et correctement formulée ?
Ne dois-je pas faire un tableau ou utilisé un symbol comme union ou inter ?
Entre les crochés c'est bien des virgules que je doit mettre et pas des point-virgules ?

[Babe]

La fontction est continu car c'est un quotient de fonction continu
Ton domaine de définition est juste
tu peut ecrire ]-oo, 1/4[U]1/4, +oo[

[yannvallet]

Merci pour la réponse, j'en ai une autre (3x-1)/(2x(2x+3))
Je crois que c'est la mème réponse mais avec un autre ensemble de définition
non ? Elle aussi continue ?

[Nightmare]

Bonjour

Elle est en effet continue sur tout intervalle où elle est définie.

[BancH]

Elle est continue sur *\ {}

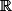
[Nightmare]

Attention Banch, on parle de continuité sur un intervalle. R*\{3/2} n'en est pas un :lol3:

[BancH]

Elle est donc continue sur l'intervalle

[Nightmare]

Elle est donc continue sur l'intervalle

Sauf que
n'est pas un intervalle mais une réunion d'intervalle :lol3:

[allomomo]

Salut,

Définition : ( si ca peut vous aider)

[Mikou]

bof, la vraie definition c'est ca il me semble : :happy3:

[Nightmare]

Il me semble même que f : A -> B est continue si l'image réciproque de tout ouver U de B est un ouvert de A :lol3:

[Mikou]

lol jtrouve plus claire le definition que jai ecrite :happy3:

[allomomo]

Et la mienne la plus simple pour un élève de terminale :)