Continuité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 02 Sep 2006, 22:34
par babaz » 02 Sep 2006, 22:34
Bonsoir,
Je vous soumets un exercice que j'ai beaucoup de mal à résoudre.
En voici l'énoncé :
"f est une fonction continue définie sur I = [0;1] telle que pour tout x de I, f(x) appartient à I.
Démontrez qu'il existe au moins un réel a de I tel que f(a) = a"
Je suis au point mort depuis pas mal de temps avec cet énoncé. Si vous pouviez donc à nouveau m'aider.
Merci
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 02 Sep 2006, 22:39
par nekros » 02 Sep 2006, 22:39
Salut,
Etudie la fonction g définie par
=f(x)-x)
puis utilise le théorème des valeurs intermédiaires.
Tu as :
=f(0)-0=f(0) \ge 0)
car
 \in [0,1])
et
=f(1)-1 \le 0)
car
 \in [0,1])
Donc on en déduit (TVI) qu'il exsite

compris entre 0 et 1 tel que
=0)
soit
-a=0)
soit
=a)
A+
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 02 Sep 2006, 22:41
par haydenstrauss » 02 Sep 2006, 22:41
a'' c'est quoi ? c'est pas la seconde dérivé de a ? ou si ? :s
EDIT :
arf dsl j'avais pas bien vu c'est la fin ds guillemenet lol
je me disait bien c'est bizzard
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 02 Sep 2006, 22:51
par haydenstrauss » 02 Sep 2006, 22:51
ha bien jouer :)
jaimerais savoir ton raisonnement.
Comment tu as eu l'idée d'étudier f(x)-x ?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 02 Sep 2006, 22:59
par nada-top » 02 Sep 2006, 22:59
salut,
Nekros--c'est surement tu voulais conclure qu'il existe
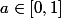
tel que
=0)
soit
-a=0)
soit
=a)
:lol5:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 02 Sep 2006, 23:00
par nekros » 02 Sep 2006, 23:00
haydenstrauss a écrit:ha bien jouer

jaimerais savoir ton raisonnement.
Comment tu as eu l'idée d'étudier f(x)-x ?
bah c'est le fait de trouver f(a)=a soit f(a)-a=0 qui met sur la piste :happy3:
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 02 Sep 2006, 23:01
par nekros » 02 Sep 2006, 23:01
nada-top a écrit:salut,
Nekros--c'est surement tu voulais conclure qu'il existe
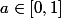
tel que
=0)
soit
-a=0)
soit
=a)
:lol5:
Oui j'ai corrigé avant d'avoir vu ton message :lol2:
a+
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 02 Sep 2006, 23:03
par haydenstrauss » 02 Sep 2006, 23:03
stp nekros ....
Comment tu as eu cette idée ? :zen:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 02 Sep 2006, 23:09
par nekros » 02 Sep 2006, 23:09
haydenstrauss a écrit:stp nekros ....
Comment tu as eu cette idée ? :zen:
Regarde le post 6 :lol4:
A+
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 02 Sep 2006, 23:11
par nada-top » 02 Sep 2006, 23:11
plutot 5 :lol5:
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 02 Sep 2006, 23:11
par babaz » 02 Sep 2006, 23:11
Merci, merci pour cette réponse instantanée !
Dans ce cas (!) j'aurais encore à un autre problème à vous soumettre (le dernier pour de la soirée, promis)
Le voici, sans guillemet :
n est un entier naturel non nul.
Démontrez que l'équation
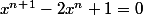
admet une racine comprise entre
/(n + 1))
et 2.
Merci !
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 02 Sep 2006, 23:13
par nekros » 02 Sep 2006, 23:13
nada-top a écrit:plutot 5 :lol5:
Décidément :ptdr:
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 02 Sep 2006, 23:19
par haydenstrauss » 02 Sep 2006, 23:19
merci j'avais pas vu
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 02 Sep 2006, 23:21
par haydenstrauss » 02 Sep 2006, 23:21
pour la deuxieme questions.
on pourrai essayer par recurence ou c'est une mauvaise idée ?
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 02 Sep 2006, 23:33
par nekros » 02 Sep 2006, 23:33
Tu peux toujours essayer aussi une étude de fonction...
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 02 Sep 2006, 23:36
par nada-top » 02 Sep 2006, 23:36
Tu peux toujours essayer aussi une étude de fonction...
par exemple
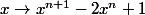
et tu applique le TVI comme a fait Nekros pour le 1er exo :lol3:
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 02 Sep 2006, 23:37
par babaz » 02 Sep 2006, 23:37
Ça me paraît assez ambitieux avec une dérivée qui équivaut à x^(n+1)((n+1).x - 2 n)
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 02 Sep 2006, 23:42
par babaz » 02 Sep 2006, 23:42
Pour tout vous dire je ne suis pas un grand habitué de ce célèbre "TVI" puisque je viens de le découvrir.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 02 Sep 2006, 23:44
par nada-top » 02 Sep 2006, 23:44
je me demande pourquoi tu cherche la dérivée :hein: je suppose que tu essaye de prouver que c'est une fonction strictement monotone mais il n'est pas demandé de prouver l'unicité mais seulement l'existence d'une telle racine, donc il suffit de voir qu'elle est continue sur
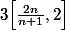
et
.f(2) \leq 0)
et tu applique le joli TVI. :lol5:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Sep 2006, 00:04
par nada-top » 03 Sep 2006, 00:04
bon voilà ,
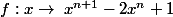
est continue sur R (fonction plynomiale) donc elle est continue sur
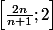
et on
 = 2^{n+1} - 2.2^n + 1 = 1)
et
 = \left(\frac{2n}{n+1}\right)^{n+1} - 2\left(\frac{2n}{n+1}\right)^n +1= \left(\frac{2n}{n+1}\right) \left(\frac{2n}{n+1}\right)^n - 2\left(\frac{2n}{n+1}\right)^n +1 \leq 0)
donc
.f\left(\frac{2n}{n+1}\right) \leq 0)
selon le TVI
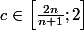
tel que
 = 0)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
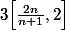 et
et .f(2) \leq 0) et tu applique le joli TVI. :lol5:
et tu applique le joli TVI. :lol5: