Continuité

[Olympus]

Donc pour chaque 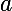, il existe au moins un intervalle ouvert où la fonction est constante . Deux cas : soit 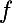est constante par morceaux, soit elle est constante sur tout 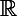. Si c'est le premier cas, alors il y aurait une infinité de points de discontinuité, contradiction vu que 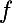est supposée être continue sur 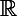d'après l'énoncé . Donc au final, elle doit être constante sur tout .

[Nightmare]

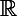C'est globalement l'idée mais deux choses sont à remarquer :

1) Ce n'est pas vrai par exemple si f est définie sur R*, il faut noter que c'est parce que R est "d'un seul tenant" que ça marche.

2) On a en fait pas besoin de la continuité de f ! Une fonction localement constante sur un ensemble "d'un seul tenant" est toujours constante.

[arnaud32]

le plus simple est surement de raisonner sur les compactes de R