Bonjour à tous!
J'essaie de réfléchir sur les liens entre continuité d'une fonction et continuité de son nombre dérivé.
J'ai d'abord pensé qu'une fonction continue sur un intervalle avait forcément sur cet intervalle un nombre dérivé continu. Ensuite, j'ai constaté que dans certains cas c'est faux, notamment quand la courbe d'une fonction fait un angle à un endroit (par exemple, la fonction "valeur absolue").
Quelqu'un sait-il donc si cela a déjà été catégorisé; si l'on sait ce qu'ont en commun les fonctions continues dont le nombre dérivé l'est aussi, et si cette catégorie de fonctions porte un nom et a des propriétés que l'on peut trouver quelque-part?
Certains rétorqueront que j'aurais dû écrire "fonction dérivable" et non "fonction continue", et "fonction dérivée", et non "nombre dérivé", mais, le problème, c'est que je souhaite justement étudier des cas limites où "le nombre dérivé est infini en un point". La fonction n'est donc pas dérivable, mais le nombre dérivé semble y exister, et c'est à lui que je m'intéresse.
Merci d'avance
Continuité du nombre dérivé
13 messages
- Page 1 sur 1
Je ne vois pas en quoi tous ces documents répondent à la question.....
Une fonction dérivable dont la dérivée est continue est une fonction de classe C1.
Je crois que la question de bastien est:
Est ce que cela apporte quelque chose de definir la nombre dérivée à valeur dans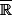 c'est à dire en autorisant comme valeur + linfini et - linfini
c'est à dire en autorisant comme valeur + linfini et - linfini
Une fonction dérivable dont la dérivée est continue est une fonction de classe C1.
Je crois que la question de bastien est:
Est ce que cela apporte quelque chose de definir la nombre dérivée à valeur dans
Bonjour Antho07!
Merci !! En dépit de mes mauvaises formulations et de mes explications approximatives, vous êtes parvenu à saisir ce qui me pose problème.
Pourriez-vous, si vous avez le temps, expliquer quelles sont les propriétés communes aux fonctions dites "de classe C1", ou, éventuellement, me donner un lien?
Pour ce qui est de ma seconde question, quelle est votre opinion?
Dans le cas simple, et même vu et revu, de la fonction racine carrée, on dit, et c'est indiscutable dit comme ça: "La pente est de plus en plus grande au fur et à mesure que l'on se rapproche de 0, et il n'existe pas de valeur de cette pente qui ne puisse être atteinte, à condition de se trouver suffisamment proche de 0." (dans la suite, j'appellerai cette proposition P1).
Ok, mais, de là, est-ce raisonnable, et cela a-t-il un sens, de faire ce que l'on fait souvent: "déduire" qu'il y a une croissance infinie en le point d'abscisse 0, "déduire" l'existence de la demi-tangente verticale en 0? Mes guillemets ne sont pas innocents: ce n'est pas à proprement parler de la déduction, il me semble que c'est plus proche de l'induction...
Alors, peut-être que de dire "Il y a virtuellement une croissance infinie en 0." (je dirai P2) signifie P1 et ne signifie rien d'autre. Si ce n'est qu'un raccourcit de langue, reconnu et maîtrisé, alors, c'est le lien entre P2 et P3 qui ne me paraît plus évident, P3 étant: "Il existe une (demie) tangente verticale en 0.". Et si c'est évident entre P3 et P2, alors il me semble que ça ne l'est plus entre P1 et P2.
Bref, passer de P1 à P3 me pose problème!
Qu'en pensez-vous?
Merci !! En dépit de mes mauvaises formulations et de mes explications approximatives, vous êtes parvenu à saisir ce qui me pose problème.
Pourriez-vous, si vous avez le temps, expliquer quelles sont les propriétés communes aux fonctions dites "de classe C1", ou, éventuellement, me donner un lien?
Pour ce qui est de ma seconde question, quelle est votre opinion?
Dans le cas simple, et même vu et revu, de la fonction racine carrée, on dit, et c'est indiscutable dit comme ça: "La pente est de plus en plus grande au fur et à mesure que l'on se rapproche de 0, et il n'existe pas de valeur de cette pente qui ne puisse être atteinte, à condition de se trouver suffisamment proche de 0." (dans la suite, j'appellerai cette proposition P1).
Ok, mais, de là, est-ce raisonnable, et cela a-t-il un sens, de faire ce que l'on fait souvent: "déduire" qu'il y a une croissance infinie en le point d'abscisse 0, "déduire" l'existence de la demi-tangente verticale en 0? Mes guillemets ne sont pas innocents: ce n'est pas à proprement parler de la déduction, il me semble que c'est plus proche de l'induction...
Alors, peut-être que de dire "Il y a virtuellement une croissance infinie en 0." (je dirai P2) signifie P1 et ne signifie rien d'autre. Si ce n'est qu'un raccourcit de langue, reconnu et maîtrisé, alors, c'est le lien entre P2 et P3 qui ne me paraît plus évident, P3 étant: "Il existe une (demie) tangente verticale en 0.". Et si c'est évident entre P3 et P2, alors il me semble que ça ne l'est plus entre P1 et P2.
Bref, passer de P1 à P3 me pose problème!
Qu'en pensez-vous?
Salut,
je crois que la manière la plus simple de voir les choses est de considérer des courbes et non des fonctions.
Par exemple on peut regarder le cercle de centre O (origine du repère) et de rayon 1.
Il est évident qu'il admet une tangente en chaque point. (C'est une courbe et même
et même  )
)
Mais si on essaye de le décrire comme y en fonction de x on a 2 fonctions
 et
et 
et aucunes d'elles n'est dérivable en 1 ni en -1.
Ceci provient simplement du fait que l'on ne peut pas écrire toutes les équations de droites sous la forme .
.
Mais une fonction peut ne pas être dérivable pour d'autres raisons : la courbe peut ne pas avoir de tangente. C'est, par exemple le cas de la fonction valeur absolue en zéro.
Et il y a des fonctions continues qui ne sont nulle part dérivables (tu peux chercher «fractales» sur internet).
En espérant avoir été utile
nuage :
je crois que la manière la plus simple de voir les choses est de considérer des courbes et non des fonctions.
Par exemple on peut regarder le cercle de centre O (origine du repère) et de rayon 1.
Il est évident qu'il admet une tangente en chaque point. (C'est une courbe
Mais si on essaye de le décrire comme y en fonction de x on a 2 fonctions
et aucunes d'elles n'est dérivable en 1 ni en -1.
Ceci provient simplement du fait que l'on ne peut pas écrire toutes les équations de droites sous la forme
Mais une fonction peut ne pas être dérivable pour d'autres raisons : la courbe peut ne pas avoir de tangente. C'est, par exemple le cas de la fonction valeur absolue en zéro.
Et il y a des fonctions continues qui ne sont nulle part dérivables (tu peux chercher «fractales» sur internet).
En espérant avoir été utile
nuage :
Bonjour,
En effet, vous réponses sont très intéressantes, merci beaucoup!
Donc, si l'on définit une fonction sur
sur 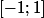 par
par =(1-x^2)^(1/2)) , il semble cohénrent et nécesaire d'admettre que sa courbe représentative possède une demie tangente verticale en -1 et une en 1.
, il semble cohénrent et nécesaire d'admettre que sa courbe représentative possède une demie tangente verticale en -1 et une en 1.
De même, si l'on définit une fonction sur
sur 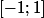 par
par =-(-1x^2)^(1/2)) , il semble cohérent et nécessaire d'admettre qe sa courbe représentative possède une demie tangente verticale en -1 et une en 1.
, il semble cohérent et nécessaire d'admettre qe sa courbe représentative possède une demie tangente verticale en -1 et une en 1.
Maintenant, définissons sur
sur 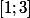 par
par =-(-1(x-2)^2)^(1/2)) - qui est en fait
- qui est en fait  décalée de deux unités vers la droite, donc, mêmes remarques pour les demies tangentes -
décalée de deux unités vers la droite, donc, mêmes remarques pour les demies tangentes -
et considérons le monstre de fonction défini sur
défini sur 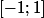 par
par =g(x)) et sur
et sur 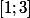 par
par =h(x)) (Si quelqu'un est capable de définir
(Si quelqu'un est capable de définir  d'une seule façon sur
d'une seule façon sur 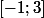 , ce sera bien mieux)
, ce sera bien mieux)
En 0, il semble que sa courbe représentative admette deux demies tangentes de même origine, de même direction (verticale), mais de sens opposés.
Question:
_ La demie tangente a-t-elle une réelle existance, de façon générale?
_ Peut-on dire qu'en 0 cette courbe admette une tangente verticale, c'est-à-dire, deux demies tangentes, est-ce bien équivalent à une tangente, au delà de l'aspect purement géométrique, où, évidemment, deux demies-droites verticales de même origine et de sens opposés forment bien une droite? (Je me suis déjà renseigné, j'ai lu des cours où l'on décrit cette singularité que sont les points d'inflexions. Mais l'on y prend presque la réponse affirmative à cette question comme axiome, et ça me gêne )
En effet, vous réponses sont très intéressantes, merci beaucoup!
Donc, si l'on définit une fonction
De même, si l'on définit une fonction
Maintenant, définissons
et considérons le monstre de fonction
En 0, il semble que sa courbe représentative admette deux demies tangentes de même origine, de même direction (verticale), mais de sens opposés.
Question:
_ La demie tangente a-t-elle une réelle existance, de façon générale?
_ Peut-on dire qu'en 0 cette courbe admette une tangente verticale, c'est-à-dire, deux demies tangentes, est-ce bien équivalent à une tangente, au delà de l'aspect purement géométrique, où, évidemment, deux demies-droites verticales de même origine et de sens opposés forment bien une droite? (Je me suis déjà renseigné, j'ai lu des cours où l'on décrit cette singularité que sont les points d'inflexions. Mais l'on y prend presque la réponse affirmative à cette question comme axiome, et ça me gêne )
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
