Arrivé là (voire avant) :
\sum\limits_{i=0}^n x^{n-i}a^{i} < \varepsilon)
Tu as plutôt intérêt à écrire (pour avoir un seul symbole < et pour que ça colle mieux avec ce qu'il faut trouver)
\sum\limits_{i=0}^n x^{n-i}a^{i}\big| < \varepsilon)
soit encore

.
Or,
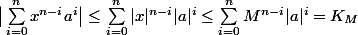
si on suppose que
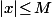
(

est indépendant de

mais dépend de

)
Donc
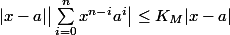
(toujours en supposant
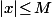
) ce qui signifie que, pour que

,
il suffit que 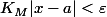
, c'est à dire que
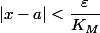
.
(attention, ce
n'est pas une condition nécessaire et suffisante, mais uniquement une condition suffisante)
On a donc pour le moment l'implication suivante :
)
Et on termine en disant qu'en prenant par exemple
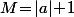
puis
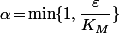
on a
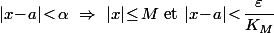
.
Ce qui permet de conclure.
Mais bon, ça serait plutôt plus court (et plus pertinent) de montrer que le produit de deux fonctions continues est continue pour en déduire ensuite que
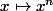
est continue comme produit de fonction continue (la fonction
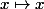
étant continue et c'est évident à démontrer).
Ce qui bien sûr n'empêche absolument pas d'essayer de le faire "à la main", ne serait ce que pour voir si on y arrive et aussi pour bien voir que c'est nettement plus simple en considérant le cas général plutôt qu'un cas particulier (i.e. en démontrant le cas général du produit de deux fonction continues plutôt que le cas particulier de la fonction
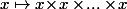
)


![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif) (je savais que tu interviendrais efficacement ... comme à ton habitude !!
(je savais que tu interviendrais efficacement ... comme à ton habitude !!