Continuité démo

par **J-R** » 31 Aoû 2007, 09:59

bonjour,

j'ai la fonction :

bien entendu cette fonction est discontinue mais comment le prouver:

si j'utilise le fait que:

je ne sais pas comment faire....

bien sur je peux le prouver avec le contre exemple mais je voudrais savoir avec cette méthode

merci

par **lapras** » 31 Aoû 2007, 10:36

salut,
si tu considérais une suite de rationnels et que tu montrais que cette suite est convergente de limite un irrationnel, donc f(Vn) = Vn car Vn est un rationnel mais si Vn tend vers un irrationnel A, alors
f(A) devrait etre égal à A, mais f(A) = 0
donc contradiction.

J'avoue que j'avais l'idée de cette suite, mais je ne sais pas laquelle choisir, et j'ai trouvé sur iledesmaths un gars qui en a trouvé une belle !
C'est dans les derniers post par "xunil", va voir :happy2:

par **J-R** » 31 Aoû 2007, 10:43

salut lapras

je sais c'est là que j'ai pris l'exo et en fait le gars il raisonne par l'absurde mais moi j'aime bien la caractérisation donnée donc si on peut trouver une démo avec ca ....:)

merci

par **Nightmare** » 31 Aoû 2007, 10:45

Bonjour, il me semble que f est continue en 0.

Puisque Q et R-Q sont denses dans R, f est continue en 0 si et seulement si :

par **J-R** » 31 Aoû 2007, 10:55

salut Nightmare,

je ne connaissais pas ce théorème, en fait ca revient à démontrer que la limite en 0 d 'un rationel doit etre égale à la limite de quoi ?

de toute facon cela prouve la continuité en 0, mais on me demande de prouver la non continuitéde cette fonction... :hum:

merci

par **Skullkid** » 31 Aoû 2007, 11:07

Bonjour, sinon pour montrer la continuité en 0 on peut procéder par encadrement :

Pour la discontinuité, j'ai pas compris ce qui te gène avec les suites, tu veux à tout prix utiliser la caractéristation formelle de la limite ? Elle n'est pas très opérationnelle pourtant...(je dis pas que c'est impossible en l'utilisant)

par **J-R** » 31 Aoû 2007, 11:11

bah en fait j'aimerais apprendre à me débrouiller avec les caractérisations de limites....

sinon pour la continuité en 0, tu le sors d'où ce théorème ?

merci

par **kazeriahm** » 31 Aoû 2007, 11:17

bah il est clair comme l'a dit skullkid que |f(x)|<=|x|

donc si x tend vers 0, f(x) tend vers 0 également. Donc

limite quand x tend vers 0 de f(x) = 0 = f(0) ce qui signifie que f est continue en 0

par **kazeriahm** » 31 Aoû 2007, 11:21

pour utiliser la définition de la continuité pour montrer la discontinuité en un point x0 donné non nul :

si x0 est rationnel, f(x0)=x0.

posons e=|f(x0)|/2.

Pour tout n>0, on peut trouver un y irrationnel dans ]x0-n,x0+n[ (car R\Q est dense dans R).

Alors f(y)=0 donc |f(x0)-f(y)|>e, ce qui montre que f est discontinue en x0.

On raisonne de meme si x0 est irrationnel en choisissant y rationnel non nul cette fois.

Tout provient du fait que Q et R\Q sont denses dans R.

par **lapras** » 31 Aoû 2007, 11:42

salut,
jolie démo, mais qu'est ce que ca signifie :

Tout provient du fait que Q et R\Q sont denses dans R.

j'ai déja entendu dire qu'il y'a une "plus grande" infinité de réels que "l'infinité des rationnels", ou quelquechose du genre

par **Nightmare** » 31 Aoû 2007, 11:45

dire que A est dense dans B veut dire que tout élément de B est limite d'une suite d'éléments de A.

Par exemple pour Q et R :

Tout réel est limite d'une suite de rationnels.

par **lapras** » 31 Aoû 2007, 11:48

Okay je comprend !
Encore me resterait il a le prouver.
C'est dur ?

par **Nightmare** » 31 Aoû 2007, 11:49

Prouver quoi? :hein:

par **lapras** » 31 Aoû 2007, 11:49

Que tout réel est limite d'une suite de rationnel.

par **Nightmare** » 31 Aoû 2007, 11:50

Ah, non tu n'y arriveras pas, niveau sup.

par **lapras** » 31 Aoû 2007, 11:51

MINCEEEE :cry: :cry:
Dur dur
Je vais devoir l'admettre !!! :cry:
Argh

par **kazeriahm** » 31 Aoû 2007, 11:52

non c'est pas trop dur, il faut parcontre le faire "à la main", ce qui rend la démo laborieuse, je pense pas que tu puisses la trouver tout seul mais tu peux la comprendre

en général, on prouve que si a et b sont deux réels distincts, on trouve un rationnel r entre a et b.

Ceci équivaut à ce que dit nightmare, dans le cas d'un ensemble totalement ordonné, ici R (c'est à dire que tout élément de R est limite d'une suite de rationnel)

Tu peux chercher sur google pour cette démo.

Une fois que tu as prouvé que Q était dense dans R, pour prouver que R\Q est également dense dans R, c'est facile :

sqrt(2) est irrationnel. Soient a et b deux réels. Comme Q est dense dans R, on peut trouver r un rationnel tel que a-sqrt(2)
Je te laisse finir :bad:

par **J-R** » 31 Aoû 2007, 11:53

merci à tous j'ai compris et dans ta démo kazeriahm on aurait pu poser e=f(xo)/p avec p un entier naturel?

deuxième question la fonction est aussi défit sur ]-oo;0] ? mais f(x) est nulle sur cet intervalle ?

a+

:++:

par **marie49** » 31 Aoû 2007, 11:55

par exemple tu prends

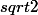
, qui est dans IR-Q .
c'est la limite de la suite :

=1

=1.4

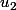
=1.41

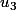
=1.414 etc...

sinon on peut aussi dire que "tout élément de IR peut être approché par un élément de Q à e près"

par **kazeriahm** » 31 Aoû 2007, 11:55

euh oui en fait tout ce que je voulais c'était que e soit strictement inférieur à f(x0), tout en étant strictement positif. On aurait pu dire soit e dans ]0,f(x0)[

Continuité démo

continuité démo

Qui est en ligne