Boss_maths a écrit:Bonjour,
Je sollicite encore votre aide sur cet exercice d'arithmétique.
Soit
\in\mathbb{N}^2)
, deux entiers naturels quelconques, on considère les nombres :
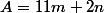
et
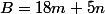
1°) Démontrer l'équivalence :
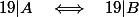
2°) On suppose
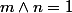
, montrer que

et

ne peuvent avoir d'autre diviseur commun que 19 et 1.
_______________________________________________
1°)

Le déterminant de ce système est :
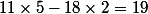
:happy3:
J'en déduis que :
\Rightarrow 19|A\\<br />19|m\text{ et }19|n\Rightarrow 19|(18m+5n)\Rightarrow 19|B<br />\right\}\quad\Rightarrow\quad 19|A\Leftrightarrow 19|B)
Alors CQFD ?
2°)
J'ai trouvé cette propriété :
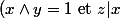\Rightarrow z\wedge y=1)
J'en déduis que :
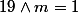
, puis la 2ème fois :
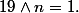
Et après... ?
Merci pour vos réponses,
@+
Moi j'aurai plutôt montré comme ça :
1°) Supposons que 19 divise A.
19 divise 11m+2n donc 19 divise 11m et 2n et par conséquent, 19 divise m et n.
Or si 19 divise m et n alors 19 divise 18m et 5n donc 19 divise 18m+5n, c'est-à-dire B.
Même raisonnement pour la réciproque :
Supposons que 19 divise B.
...
2°) Ici, à vue de nez, je raisonnerais par l'absurde :
On suppose qu'il existe un entier naturel non nul
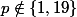
tel que

divise

.
@+
