[Arithmétique] Construire une démonstration
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Boss_maths
- Membre Naturel
- Messages: 82
- Enregistré le: 11 Déc 2010, 08:24
-
 par Boss_maths » 15 Aoû 2012, 14:49
par Boss_maths » 15 Aoû 2012, 14:49
Bonjour/soir,
Je sollicite votre aide pour cet exercice d'arithmétique.
Soit

, un entier naturel quelconque, on considère les nombres :
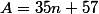
et
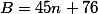
Démontrer que
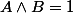
ou
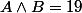
_____________________________________
Si j'ai remarqué que :
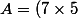n+3\times 19)
et
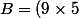n+4\times 19)
,
je ne sais pas comment, à l'aide des propriétés de la divisibilité, poursuivre la démonstration :wrong:
Merci par avance,
@+
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 15 Aoû 2012, 14:58
par Skullkid » 15 Aoû 2012, 14:58
Bonjour, si je te demandais de me calculer le pgcd de 527 et 804, tu ferais comment ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Aoû 2012, 15:16
par chan79 » 15 Aoû 2012, 15:16
Boss_maths a écrit:Bonjour/soir,
Je sollicite votre aide pour cet exercice d'arithmétique.
Soit

, un entier naturel quelconque, on considère les nombres :
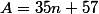
et
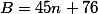
Démontrer que
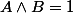
ou
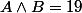
_____________________________________
Si j'ai remarqué que :
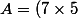n+3\times 19)
et
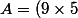n+4\times 19)
,
je ne sais pas comment, à l'aide des propriétés de la divisibilité, poursuivre la démonstration :wrong:
Merci par avance,
@+
Salut
Soit un entier p qui divise A et B.
Compte tenu de ce que tu as remarqué, tu peux écrire que p divise 9A et 7B
-
Boss_maths
- Membre Naturel
- Messages: 82
- Enregistré le: 11 Déc 2010, 08:24
-
 par Boss_maths » 15 Aoû 2012, 15:39
par Boss_maths » 15 Aoû 2012, 15:39
Skullkid a écrit:Bonjour, si je te demandais de me calculer le pgcd de 527 et 804, tu ferais comment ?
Merci pour ta réponse.
Aucun diviseur commun entre 804 et 517, donc pgcd=1 ?
@+
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 15 Aoû 2012, 15:53
par Skullkid » 15 Aoû 2012, 15:53
Boss_maths a écrit:Merci pour ta réponse.
Aucun diviseur commun entre 804 et 517, donc pgcd=1 ?
@+
J'en sais rien, j'ai pris les nombres au hasard, le but du jeu était de les prendre suffisamment grands pour te décourager d'essayer de lister les diviseurs, mais ça n'a pas marché (sinon, il y a toujours au moins un diviseur commun à deux entiers : 1). Quand on te demande de calculer le pgcd de deux nombres, tu dois penser à l'algorithme d'Euclide. Essaye donc cet algorithme sur A et B (ou suis la piste, plus astucieuse, de chan79).
-
Boss_maths
- Membre Naturel
- Messages: 82
- Enregistré le: 11 Déc 2010, 08:24
-
 par Boss_maths » 15 Aoû 2012, 16:05
par Boss_maths » 15 Aoû 2012, 16:05
chan79 a écrit:Salut
Soit un entier p qui divise A et B.
Compte tenu de ce que tu as remarqué, tu peux écrire que p divise 9A et 7B
Merci pour ta réponse.
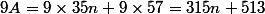
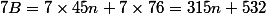
Je remarque que 9A<7B et comme :
\quad\Rightarrow\quad(p|7B-9A)\quad\Rightarrow\quad(p|532-513=19))
un nombre premier.
Je remarque des choses, mais ce n'est pas la démonstration :doute2:
@+

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Aoû 2012, 17:10
par chan79 » 15 Aoû 2012, 17:10
Boss_maths a écrit:Merci pour ta réponse.
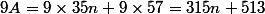
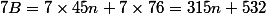
Je remarque que 9A<7B et comme :
\quad\Rightarrow\quad(p|7B-9A)\quad\Rightarrow\quad(p|532-513=19))
un nombre premier.
Je remarque des choses, mais ce n'est pas la démonstration :doute2:
@+
le pgcd de A et B divise 19 donc ...
-
Boss_maths
- Membre Naturel
- Messages: 82
- Enregistré le: 11 Déc 2010, 08:24
-
 par Boss_maths » 15 Aoû 2012, 17:53
par Boss_maths » 15 Aoû 2012, 17:53
chan79 a écrit:le pgcd de A et B divise 19 donc ...
Ben, ce qui me gêne c'est que p est un diviseur de 19, mais pourquoi p serait le pgcd de 9A et 7B et de la différence et... ?
Merci et @+

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Aoû 2012, 18:28
par chan79 » 15 Aoû 2012, 18:28
Boss_maths a écrit:Ben, ce qui me gêne c'est que p est un diviseur de 19, mais pourquoi p serait le pgcd de 9A et 7B et de la différence et... ?
Merci et @+
le pgcd de A et B divise aussi les nombres suivants: 9A, 7B, 9A-7B
si un nombre en divise deux autres, il divise aussi leur différence
-
Boss_maths
- Membre Naturel
- Messages: 82
- Enregistré le: 11 Déc 2010, 08:24
-
 par Boss_maths » 15 Aoû 2012, 19:05
par Boss_maths » 15 Aoû 2012, 19:05
chan79 a écrit:le pgcd de A et B divise aussi les nombres suivants: 9A, 7B, 9A-7B
si un nombre en divise deux autres, il divise aussi leur différence
Ok, je crois avoir saisi ce qui me manquait pour... comprendre ?
Au départ, en hypothèse, on se dit que p est un diviseur, mais pas n'importe lequel c'est le pgcd !
Après, le raisonnement sur la divisibilité je connaissais :
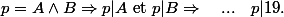
Mais comme 19 est premier, alors :
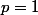
ou
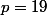
, CQFD !?
@+

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Aoû 2012, 19:24
par chan79 » 15 Aoû 2012, 19:24
Boss_maths a écrit:Ok, je crois avoir saisi ce qui me manquait pour... comprendre ?
Au départ, en hypothèse, on se dit que p est un diviseur, mais pas n'importe lequel c'est le pgcd !
Après, le raisonnement sur la divisibilité je connaissais :
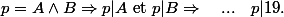
Mais comme 19 est premier, alors :
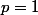
ou
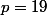
, CQFD !?
@+
oui, c'est ça
on remarque que le pgcd de A et B est 19 si n est un multiple de 19 et sinon, c'est 1
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 17 Aoû 2012, 09:57
par egan » 17 Aoû 2012, 09:57
Ya une méthode un peu moins fatiguante pour le cerveau pour faire ce genre de trucs.
Tu peux même améliorer un peu le résultat que tu proposes de démontrer.
On définit la fonction
 = (35n+57) \wedge (45n+76))
sur

ou

.
Alors on a:
 = (45n+76) \wedge (35n+57))
 = (10n+19) \wedge (35n+57))
 = (35n+57) \wedge (10n+19))
 = (5n) \wedge (10n+19))
 = (10n+19) \wedge (5n))
 = 19 \wedge (5n))
 = (5n) \wedge 19)
 = n \wedge 19)
Et voilà, tu sais donc que

ne peut prendre que les valeurs 1 et 19.
Et là où tu améliores ton résultat, c'est que tu as aussi montré par la même occasion que

est 19-périodique !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
