Conseils pour résoudre ce problème

[hugo]

Dans le plan muni d'un repère orthonormal(O;i;j), on considère la parabole P d'équation y=x^2-4x+5
J'ai tracé la parabole
Ensuite,l'énoncé se poursuit par:
Soit A le point de coordonnées(1;3)et deltam,la droite passant par le point A et de coefficient directeur m.On note M1 et M2 les points d'intersection de delta m et de P
Démonter que les abscisses des pointsM1 et M2 sont les solutions de l'équation:x^2-(4+m)x+(m+2)=0
Ma question est comment trouve -t'on le coefficient directeur?
Je pense que delta m est d'équation y=x+3 et le coeff directeur serait
alors 1 mais je n'en suis pas sûr!!
pourriez vous me mettre sur la piste?s'il vous plait!merci d'avance!!

[fonfon]

salut, ici il n'y a pas besoin de chercher le coefficient directeur de il te le donne c'est m donc ta droite est de la forme :

y=mx+b or elles passe par A(1,3) donc les coordonnées de A verifient l'equation de donc on remplace

3=1*m+b b=3-m

donc a pour equation

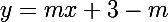
sinon

pour calculer le coefficient directeur d'une droite (AB) non parallele à l'axe des ordonnées c'est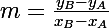 pour une droite de la forme y=mx+p

[fonfon]

Re,

on te dit que:

On note M1 et M2 les points d'intersection de delta m et de P

ben pour trouver les coordonnees de M1 et M2 il faut resoudre:









donc comme les points M1 et M2 sont les points d'intersectiond de P et deltam alors ils verifient bien l'equation y=x²-(4+m)x+m+2=0