Conjugué d'un nombre complexe

[TheworstMatheu]

Bonjour, je vous explique ma situation, je suis en Terminale S mais ce trimestre c'est complétement lâché les maths ( oui grossière erreur) et maintenant je me retrouve avec un exercice a faire dont je n'ai pas la moindre idée de solution, le voici:

"Z et Z' sont deux nombres complexes tels que ZZ' [Différent] de -1 et |Z'|=1
Démontrer que le nombre (Z+Z')/(1+ZZ') est un nombre réél "

Quelqu'un peut me donner un coup de pouce s'il vous plait? :/

[Sylviel]

Pour montrer qu'un nombre est réel il y a trois solution :
- montrer que sa partie imaginaire est nulle
- montrer que son argument est 0 modulo pi (ou que le nombre est nul)
- montrer qu'il est égal à son conjugué.

Quel technique employer ici a priori ?

[TheworstMatheu]

Mhhh n'ayant rien compris de la façon de procédé, a tout hasard:

- montrer que son argument est 0 modulo pi (ou que le nombre est nul) ?

[Sylviel]

Non... (mais ici ce n'est pas facile de le voir)

En gros il y a trois manière de gérer les complexes :
- leur forme algébrique a+ib
- leur forme exponentielle r e^(i theta)
- directement sous forme complexe, en utilisant le conjugué.

la forme algébrique est la méthode par défaut
la forme explonentielle est particulièrement adaptée aux puissances, divisions, argument, ...
la méthode complexe est utile lorsque l'on a des infos sur le conjugué du complexe.

Ici c'est la troisième méthode qu'il faut employer (en effet |z|=1 signifie que |z|²=1, donc que conj(z)=1/z). Pour t'aider le premier reflexe a avoir quand tu voies |z|=1 c'est de le remplacer par z=e^i theta. Ensuite tu calcules le conjugué de ton quotient et essaie de retomber sur tes pattes :-)

P.S : cet exo n'est pas un exercice "facile" (sans être super méga hardcore non plus ^^).

[TheworstMatheu]

Ici c'est la troisième méthode qu'il faut employer (en effet |z|=1 signifie que |z|²=1, donc que conj(z)=1/z). Pour t'aider le premier reflexe a avoir quand tu voies |z|=1 c'est de le remplacer par z=e^i theta. Ensuite tu calcules le conjugué de ton quotient et essaie de retomber sur tes pattes

Attention c'est |z'| qui est égal a 1, je ne sais pas si cela change quelque chose

P.S : cet exo n'est pas un exercice "facile" (sans être super méga hardcore non plus ^^).

Mouai sa depend du point de vue ça ^^'

[Sylviel]

Non ça ne change rien, essaie de faire ce que je t'ai dis :
ecris z' sous forme e^i theta
calcule le conjugué de ton quotient

[TheworstMatheu]

Non ça ne change rien, essaie de faire ce que je t'ai dis :
ecris z' sous forme e^i theta
calcule le conjugué de ton quotient

Pour avoir théta il faut bien que je trouve le sin théta et le cos théta c'est ça? Grace a z/module et x/module?

[Sylviel]

non non pas besoin d'avoir theta. C'est un nombre, il sert à représenter z'.

[Sylviel]

Je te donnes un exemple de résolution pour ton exercice :
montrer que est réel. On calcule

donc Z est réel.

Tu fais le même avec ton quotient...

[TheworstMatheu]

montrer que est réel. On calcule


Bon j'ai essayé votre méthode et sa me donne un Galimatias tel que ça:




? :mur: :mur: :mur: :mur:

[TheworstMatheu]

En plus je fail mon écriture --'

[Sylviel]

Ok c'est pas mal, maintenant il faut essayer d'exploiter la condition |z'|=1 (j'ai déjà rapellé là haut comment).

P.S : j'ai l'impression qu'il faut que |z|=1 aussi, ce n'est pas le cas ?

[TheworstMatheu]

P.S : j'ai l'impression qu'il faut que |z|=1 aussi, ce n'est pas le cas ?

En effet |z|=|z'|=1

Mhhh pour ce qui est d'exploité de |Z'|=1 ...
Juste une question, quel est la différence entre \bar{z'} et |z'|?

[Sylviel]

Ca n'a rien à voir :briques:
|z| c'est le module de z, c'est la distance entre l'origine et l'affixe sur le plan...
|z|²=a²+b² si z=a+ib (c'est juste pythagore cette formule), etc...
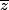c'est le conjugué, c'est à dire le symétrique par rapport à l'axe Ox, ou encore a-ib.

Remonte un peu dans les posts et trouve moi comment on peut exploiter |z|=1.

[TheworstMatheu]

J'ai beau regarder l'équation et la tordre dans tout les sens, je ne vois pas --' Un coup de pouce magique? :D :stupid:

[TheworstMatheu]

.... je sais que je ne suis pas bon mais si je n’essaie pas de comprendre je n'y arriverai jamais

[cbmaths]

Bonjour,

tu as déjà trouvé :

En tenant compte du fait que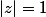 tu as donc , cette propriété des nombres complexes de module 1 est à retenir, elle peut servir dans d'autres exercices.

Ainsi, et , il ne te reste plus qu'à remplacer dans l'expression de 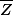que tu as déjà trouvée, ensuite simplifie le calcul pour retrouver .

[TheworstMatheu]

C'est bon j'ai réussi! Mouhahahha merci bien a vous deux :D