bonsoir,
j'ai un peu de mal avec cet exercice:
On considère la suite définie par U0 = 2 et, pour tout entier naturel n Un+1 = -Un² + 2Un + 1
Conjecturer une propriété de la suite (Un), puis démontrer cette propriété par récurrence.
J'ai calculeé les termes successifs de la suite et je trouve U0 = 2 U1 = 1 U2 = 2 U3 = 1 U4 = 2 etc...
on peut donc voir que:
pour tout n pair on a "2" un chiffre pair,
pour tout n impair on a "1" un chiffre impair
Le pb, j'ai essayé plein de formules, mais je n'arrive pas à trouver Un en fonction de n :s
Merci de votre aide !
Conjecturer une suite
11 messages
- Page 1 sur 1
Tu as 2 possibilités
Soit tu choisis pour propriété de récurrence
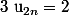 et
et 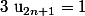
Auquel cas, l'initialisation se fait avec et
et 
Et l'hérédité se fait en supposant que
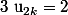 et
et 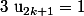
et en montrant que
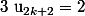 et
et 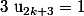
Soit tu choisis pour propriété de récurrence
^n}{2})
Auquel cas, l'initialisation se fait avec
Et l'hérédité se fait en supposant que
^k}{2})
et en montrant que
^{k+1}}{2})
Soit tu choisis pour propriété de récurrence
Auquel cas, l'initialisation se fait avec
Et l'hérédité se fait en supposant que
et en montrant que
Soit tu choisis pour propriété de récurrence
Auquel cas, l'initialisation se fait avec
Et l'hérédité se fait en supposant que
et en montrant que
Parce que la propriété de récurrence est P(n) : 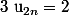 et
et 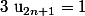
La propriété porte sur 2 termes
Donc pour vérifier P(0), il faut vérifier que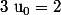 et
et 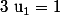
Si tu trouves ça trop compliqué tu peux faire 2 récurrences disjointes
P(n) :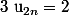
Tu initialises avec
Et tu montres que si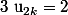 alors
alors 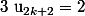
Ce qui prouve la 1ère récurrence
Et ensuite tu fais la 2ème récurrence
Q(n) :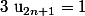
La propriété porte sur 2 termes
Donc pour vérifier P(0), il faut vérifier que
Si tu trouves ça trop compliqué tu peux faire 2 récurrences disjointes
P(n) :
Tu initialises avec
Et tu montres que si
Ce qui prouve la 1ère récurrence
Et ensuite tu fais la 2ème récurrence
Q(n) :
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
