Conjecturer et recurrence
14 messages
- Page 1 sur 1
Conjecturer et recurrence
Bonsoir à tous,
voila je bloque sur un exercice et j'aimerai bien que l'on m'éclaircisse un peu.
Voici l'énoncé:
On considère la suite (Un) définie par Uo = 1 et pour tout entier naturel n par Un_+1 = 10Un - 9n - 8
1)Calculer de U1 à U4
2)Conjecturer une expression de Un en fonction de n.
3)Démontrer cette conjecture par récurrence
Pour la question 1) je trouve:
U1= -7
U2= -96
U3= -995
U4= -99993
Mais je bloque sur les deux autres questions.
Merci de m'aider.
voila je bloque sur un exercice et j'aimerai bien que l'on m'éclaircisse un peu.
Voici l'énoncé:
On considère la suite (Un) définie par Uo = 1 et pour tout entier naturel n par Un_+1 = 10Un - 9n - 8
1)Calculer de U1 à U4
2)Conjecturer une expression de Un en fonction de n.
3)Démontrer cette conjecture par récurrence
Pour la question 1) je trouve:
U1= -7
U2= -96
U3= -995
U4= -99993
Mais je bloque sur les deux autres questions.
Merci de m'aider.
MacManus a écrit:Oui c'est ça :
C'est une suite arithmétique de raison:
Cependant, je dois prouver mon résultat par récurrence.
J'ai fait la phase d'initiation, mais je ne sais pas de quoi partir pour l'hérédité.
Je sais que pour montrer légalité on part de Un+1=... mais je ne sais pas qu'elle est l'hypothèse de récurrence ni ce que je dois mettre à la place des ...
Merci de me donner un dernier coup de pouce ^^
PS: est ce que Un+1= Un+1 + 1 est égale à Un+2?
Car j'ai fait, Un= n + 1 alors montrons que Un+1= Un+1 + 1
Un+1= 10Un-9n-8 = 10(n +1)-9n-8 = n + 2
Soit Un+1 = n+2
Est-ce bon ?
C'est important effectivement de bien maîtriser les étapes dans une démonstrations par réccurence :
initialisation
 (pas de pb)
(pas de pb)
hérédité
On suppose la relation vraie pour un certain entier k : c'est notre hypothèse de récurrence. Il faut montrer que cette propriété est également vraie au rang k+1. C'est-à-dire que l'on veut montrer que
vraie pour un certain entier k : c'est notre hypothèse de récurrence. Il faut montrer que cette propriété est également vraie au rang k+1. C'est-à-dire que l'on veut montrer que ) . On sait aussi que
. On sait aussi que  . Tu peux donc remplacer
. Tu peux donc remplacer 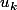 par
par  dans
dans 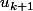 . Ok ??
. Ok ??
initialisation
hérédité
On suppose la relation
MacManus a écrit:C'est important effectivement de bien maîtriser les étapes dans une démonstrations par réccurence :
initialisation(pas de pb)
hérédité
On suppose la relationvraie pour un certain entier k : c'est notre hypothèse de récurrence. Il faut montrer que cette propriété est également vraie au rang k+1. C'est-à-dire que l'on veut montrer que
. On sait aussi que
. Tu peux donc remplacer
par
dans
. Ok ??
Vous trouvez donc Uk+1= k+2 comme moi ?
Il faut donc bien que je mette Uk+1= Uo + (k+1) ou ma méthode marche aussi ?
Encore merci !
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
