Conjecture a verifier...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 24 Oct 2007, 13:24
par gol_di_grosso » 24 Oct 2007, 13:24
a=k(k+3) b=1
^2<br />\\=(a+b) (a+b)<br />\\=a^2+2ab+b^2<br />\\=(k(k+3))^2+2k(k+3) +1^2<br />\\=k^2(k+3)^2+2k(k+3)+1)
ça va là ?
bon après tu factorise pas k(k+3)
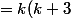 (k(k+3)+2)+1<br />\\=k(k+3) (k^2+3k+2)+1)
ensuite
=(k+1)(k+2))
c'est touvable
donc
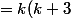(k+1)(k+2)+1)
donc
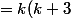(k+1)(k+2)+1=(k(k+3)+1)^2)
-
spirou974
- Membre Naturel
- Messages: 21
- Enregistré le: 24 Oct 2007, 08:57
-
 par spirou974 » 24 Oct 2007, 13:24
par spirou974 » 24 Oct 2007, 13:24
stp thales si pour toi c'est clair partage ton savoir avec nous :we:
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 24 Oct 2007, 13:25
par gol_di_grosso » 24 Oct 2007, 13:25
toujours pas clair ?
-
spirou974
- Membre Naturel
- Messages: 21
- Enregistré le: 24 Oct 2007, 08:57
-
 par spirou974 » 24 Oct 2007, 13:27
par spirou974 » 24 Oct 2007, 13:27
b=+1 c ca?
-
spirou974
- Membre Naturel
- Messages: 21
- Enregistré le: 24 Oct 2007, 08:57
-
 par spirou974 » 24 Oct 2007, 13:28
par spirou974 » 24 Oct 2007, 13:28
stp tu peux repondre a nos question en debut de page stp?
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 24 Oct 2007, 13:33
par gol_di_grosso » 24 Oct 2007, 13:33
bonjour j ai un exercice a rendre que je ne comprend pas tres bien !!j aurais besoin d aide si vous pouvais m aider???
Le proffeseur a remarque que
1x2x3x4+1=25=5²
2x3x4x5+1=121=11²
3x4x5x6+1=361=19²
...........etc il pense pouvoir enoncer une propriete generales
"quand on multiplie par 4 entiers naturels consecutifs non nuls et que l on ajoute 1 = k(k+1)(k+2)(k+3)+1 c'est bon ça ?
au resultat on obtient le carre d un nombre entier!!"
ba oui c'est (k(k+3))² avec d=k(k+3)
donc ça c'est vrai
il dirai meme plus on obtient le carre d un nombre premier
ça c'est faux pour k=6 d=55 =5*11
-
Thalès
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Fév 2007, 19:51
-
 par Thalès » 24 Oct 2007, 13:37
par Thalès » 24 Oct 2007, 13:37
Bon j'éspère que mon explication sera plus claire pour vous :)
on cherche à démontrer que : k(k+1)(k+2)(k+3)+1 = (k(k+3)+1)²
on a : (k(k+3)+1)² = [k(k+3)]²+2[k(k+3)]+1 (l'identité remarquable (a+b)² en supposant que a=k(k+3) et b=1, maintenant on factorise par k(k+3) pour les deux premiers termes :
(k(k+3)+1)² = [k(k+3)]²+2[k(k+3)]+1 = [k(k+3)][k(k+3)+2]+1
d'où : = [k(k+3)](k²+3k+2) +1 j'ai juste développer le k(k+3)
Tu peux remarquer que :
k²+3k+2 = k²+2k+1+k+1 =(k+1)²+(k+1) = (k+1)(k+1+1)=(k+1)(k+2)
d'où : = k(k+3)(k+1)(k+2)+1 et puisque le produit est commutatif :
=k(k+1)(k+2)(k+3)+1
-
spirou974
- Membre Naturel
- Messages: 21
- Enregistré le: 24 Oct 2007, 08:57
-
 par spirou974 » 24 Oct 2007, 13:40
par spirou974 » 24 Oct 2007, 13:40
oui mais le resultat k^4+6k^3+11k^2+6k il est faux??(c'est ce que j'ai trouvé )
-
tytony1313
- Membre Naturel
- Messages: 21
- Enregistré le: 16 Oct 2007, 07:55
-
 par tytony1313 » 24 Oct 2007, 13:43
par tytony1313 » 24 Oct 2007, 13:43
il dirai meme plus on obtient le carre d un nombre premier
ça c'est faux pour k=6 d=55 =5*11
euuuu??????????
-
spirou974
- Membre Naturel
- Messages: 21
- Enregistré le: 24 Oct 2007, 08:57
-
 par spirou974 » 24 Oct 2007, 13:45
par spirou974 » 24 Oct 2007, 13:45
d c'est quoi?
-
Thalès
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Fév 2007, 19:51
-
 par Thalès » 24 Oct 2007, 13:52
par Thalès » 24 Oct 2007, 13:52
d=k(k+3)+1
-
spirou974
- Membre Naturel
- Messages: 21
- Enregistré le: 24 Oct 2007, 08:57
-
 par spirou974 » 24 Oct 2007, 13:55
par spirou974 » 24 Oct 2007, 13:55
merci beaucoup
-
Thalès
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Fév 2007, 19:51
-
 par Thalès » 24 Oct 2007, 13:57
par Thalès » 24 Oct 2007, 13:57
spirou974 a écrit:oui mais le resultat k^4+6k^3+11k^2+6k il est faux??(c'est ce que j'ai trouvé )
Oublie ce raisonnement, si tu as compris la méthode de gol di grosso c'est bon
-
spirou974
- Membre Naturel
- Messages: 21
- Enregistré le: 24 Oct 2007, 08:57
-
 par spirou974 » 24 Oct 2007, 14:52
par spirou974 » 24 Oct 2007, 14:52
ok merci c simpa
-
spirou974
- Membre Naturel
- Messages: 21
- Enregistré le: 24 Oct 2007, 08:57
-
 par spirou974 » 24 Oct 2007, 14:57
par spirou974 » 24 Oct 2007, 14:57
gol_di_grosso a écrit:il dirai meme plus on obtient le carre d un nombre premier
ça c'est faux pour k=6 d=55 =5*11
je n'ai pas bien compris cela
-
Thalès
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Fév 2007, 19:51
-
 par Thalès » 24 Oct 2007, 16:02
par Thalès » 24 Oct 2007, 16:02
Ce n'est pas gol di grosso qui a dit ça mais plutôt tytony1313
Il veut dire qu'on ne trouve pas toujours un nombre premier de la forme :k(k+3)+1 = rac[k(k+1)(k+2)(k+3)+1]
La preuve, il a pris comme exemple k=6, donc :
k(k+3)+1 = 6(6+3)+1 = 6.9+1=54+1=55
55 n'est pas un nombre premier car il est divisible par 5 et par 11
PS : rac[k(k+1)(k+2)(k+3)+1] veut dire la racine carrée de k(k+1)(k+2)(k+3)+1
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 24 Oct 2007, 16:40
par gol_di_grosso » 24 Oct 2007, 16:40
merci Thalès
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités