bonjour j'ai un exo sur les congruences et je galère a le resoudre car j'ai du mal à voir quelle méthode il faut utiliser voici l'énoncé:
on pose: A=10^(9n)+2*10^(6n)+2*10^(3n)+1
1.a.trouver suivant les valeurs de n , le reste de la division de 10^n par 111.
j'ai trouvé: si n=3k alors le reste est 1 si n=3k+1 le reste est 10 et si n=3k+2 alor le reste est 100
b. déduisez en le reste de la division de A par 111
2.a.on suppose n impair. Démontrez que A est divisible par 7, par 11 et par 13.
b. on supose n est pair. Démontrez que A a le même reste dans les divisions par 7, par 11 et par 13.
je suis perdue!
j'espère que vous pourrez m'aider!!
merci d'avance!!
Congruences :'(
3 messages
- Page 1 sur 1
Quand tu as plusieurs congruences (modulo le même nombre bien sûr), tu peux les additionner, soustraire, multiplier ou élever à une puissance comme tu veux (je marque pas (mod p) pour faire plus court):
Si et
et  , alors
, alors  ,
,  , pour tout n dans N,
, pour tout n dans N,  , pour tout k
, pour tout k  , ce sont ces propriétés qu'on utilise en général pour calculer les congruences.
, ce sont ces propriétés qu'on utilise en général pour calculer les congruences.
Pour le 1b, A s'écrit comme une somme avec des puissances de 10, or tu as calculé le reste de la division par 111 pour les puissances de 10, et là les exposants sont tous de la forme 3k, , il suffit de remplacer les puissances de 10 par des 1 dans A pour trouver le reste :
, il suffit de remplacer les puissances de 10 par des 1 dans A pour trouver le reste :

Pour la question 2 c'est un peu pareil, on cherche à calculer pour p valant 7, 11, 13 en cherchant d'abord ce que vaut
pour p valant 7, 11, 13 en cherchant d'abord ce que vaut  puis en regardant des petites puissances :
puis en regardant des petites puissances :
pour 11 : donc on remplace les 10 par -1 pour calculer le reste, le résultat dépend donc de la parité de n.
donc on remplace les 10 par -1 pour calculer le reste, le résultat dépend donc de la parité de n.
pour 7 : , on sait pas bien calculer
, on sait pas bien calculer  donc on regarde les puissances :
donc on regarde les puissances :

 , et on peut faire le calcul avec ça vu que
, et on peut faire le calcul avec ça vu que ^n) .
.
Pour 13 c'est la même technique qu'avec 7.
Si
Pour le 1b, A s'écrit comme une somme avec des puissances de 10, or tu as calculé le reste de la division par 111 pour les puissances de 10, et là les exposants sont tous de la forme 3k,
Pour la question 2 c'est un peu pareil, on cherche à calculer
pour 11 :
pour 7 :
Pour 13 c'est la même technique qu'avec 7.
Bonsoir
1.b les 3 exposants sont des multiples de 3; D'après la question précédente quand on divise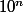 par 111 , le reste est 1 quand n est multiple de 3, soit
par 111 , le reste est 1 quand n est multiple de 3, soit )
Par conséquent , modulo 111,
Quand on divise A par 111, le reste est donc 6.
2. a) Modulo 7 ,) car en divisant 1000 par 7 , le reste est 6 et
car en divisant 1000 par 7 , le reste est 6 et \ mod 7)
^{3n}+2(10^3)^{2n}+ 2(10^3)^n+1)
donc modulo 7,^{3n}+2(-1)^{2n}+2(-1)^n+1=-1+2-2+1=0) (car 3n et n sont impairs tandis que 2n est pair), ce qui prouve que A est divisible par 7.
(car 3n et n sont impairs tandis que 2n est pair), ce qui prouve que A est divisible par 7.
De même\ (mod 11)) et le calcul est identique.
et le calcul est identique.
A est divisible par 11
De même\ (mod 13)) même calcul à nouveau.
même calcul à nouveau.
b) Si n est pair , 3n, 2n et n sont pairs donc^{3n}+2(-1)^{2n}+2(-1)^n+1=1+2+2+1=6\ (mod 7))
Le reste de la division de A par 7 est donc 6 et le calcul est le même pour les divisions par 11 et 13.
1.b les 3 exposants sont des multiples de 3; D'après la question précédente quand on divise
Par conséquent , modulo 111,
Quand on divise A par 111, le reste est donc 6.
2. a) Modulo 7 ,
donc modulo 7,
De même
A est divisible par 11
De même
b) Si n est pair , 3n, 2n et n sont pairs donc
Le reste de la division de A par 7 est donc 6 et le calcul est le même pour les divisions par 11 et 13.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
