Congruences et multiplication de "modulo"

[GeorgeB]

Bonjour, j'ai encore un exercice d'arithmétique sur lequel je bloque:


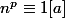
Soit PGCD(a,b)=1 et ainsi que

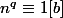
Comment montrer que avec d=PGCD(p,q) on a

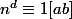
merci !!

[Doraki]

On peut pas.

Mais si d = PPCM(p,q), on peut.

[GeorgeB]

c'est pourtant l'énoncé de mon livre ... ou y a-il un problème ?

[Ben314]

Fait un essai, ça ne coute rien...
Prend par exemple n=2, a=3 et b=7 (qui sont bien premiers entre eux)
Cherche le plus petit p tel que 2^p=1 modulo 3
puis le plus petit q tel que 2^q=1 modulo 7
puis regarde si 2^r=1 modulo 3*7 en prenant r=pgcd(p,q) ?
et en prenant r=ppcm(p,q) comme le conseille Doraki ?

[GeorgeB]

Oui vous avez raison ! Fichu livre !