Congruences avec inconnues en exposant

[kadaid]

Bonjour
Les inconnues sont x et y entières
J'ai cherché sur internet des exos du genre: a^(ux+q) + b^(u'y+q') =...(n), (modulo n)
puis on se ramène à la forme: c^(rx+s)+c^(r'y+s')=...(n) de façon à se ramener à la forme:
rx+s+r'y+s'=k*n, k entier, mais j'ai rien trouvé.
Je ne sais pas si c'est bien clair!

Merci pour vos commentaires.

[Ben314]

Salut,
Bon, déjà, je te rassure vu que tu semble avoir des doutes : c'est pas super clair...

Par contre, bien que ce soit pas clair, ton laïus donne l'impression que tu pense qu'une équation de la forme (a,b,n connus ; x inconnu) est équivalente à un truc de la forme avec le même dans les deux équations et... c'est totalement faux...
Fait un tableau pour évaluer les différentes valeurs de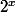 modulo 5 pour (entier) de 0 à 15 puis dit moi quelle sont les solutions entières positives (*) de l'équation .

(*) Je ne pense pas qu'à ton niveau ça ait du sens de chercher les solutions entière négatives.

P.S. je note [n] à la fin pour traduire "modulo n" (les notation ne sont pas super standardisées...)

[kadaid]

Bonjour Ben314
Oui, j'ai rédigé mon message pas en français mais en "charabia"!
Mais tu as deviné l'essentiel, on en reparlera après de ce que je voulais.

Réponse à ton équation: 2^x=3[5]
restes={1;2;4;3} pour x={0;1;2;3;....}
La suite des restes est périodique, de période 4.
2^3=3[5]
2^7=3[5]
2^11=3[5]
2^15=3[5]
Solution générale: x=4k-1, k entier, k>0
pour k=0, on a une puissance négative (x=-1) et là je n'en sais rien!

[Ben314]

C'est bien ça et ça signifie que, pour tout entier positif x, on a :

C'est à dire que le modulo 5 de l'équation de départ est devenu un modulo 4 dans le résultat final donc on a "changé de congruence" lorsque l'on a "fait descendre le x de l'exposant".

Au niveau Lycée, il y a pas mal d'exercice de ce type où on constate effectivement ce fait, mais la théorie qu'il y a derrière est un peu compliquée.
Je pense qu'au mieux, ce qu'on pourrait faire au niveau Lycée, c'est de montrer que, si est un nombre premier, alors une équation de la forme , si elle a des solutions, ces dernières seront de la forme où l'entier est un diviseur de 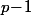(mais même ça, c'est pas facile du tout).

[kadaid]

Alors je reviens à mon premier message ou' je voulais parler d'une équation congruence à deux inconnues x et y qui sont en exposant:
Par exemple, en ajoutant 7^y à ton équation , on aura l'équation suivante à résoudre:
2^x+7^y=...[5]

Je n'ai jamais étudié ce genre d'équation mais je suis curieux de voir comment ça se passe, bien sûr avec une aide.

[zygomatique]

ben donne un exemple concret ...

[kadaid]

2^x+7^y=a[5]
Le problème, je ne sais pas choisir a pour que l'équation ait des solutions.
Comme je l'ai expliqué dans mon message précédent, j'aimerais qu'on me donne une équation de ce genre avec une aide!

[Ben314]

Avec un truc pareil, au niveau lycée, y'a pas 36 000 trucs à faire : il faut calculer les 2^x pour x=0,1,2,3,4,... jusqu'à ce qu'on trouve quelle est la "logique" là dedans (en particulier quelles sont les différentes valeur que l'on peut avoir) puis la même chose pour les 7^y (sauf qu'ici, vu que 7=2 [5], 7^y=2^y [5] donc c'est les mêmes valeurs que précédemment)
Ensuite, pour un a "variable", ça va pas trop être faisable au niveau Lycée, mais par exemple avec a=2, ben tu regarde toute les façons possible et imaginable de faire X+Y=2 [5] où X est un des nombre qui apparaisse dans la suite des 2^x et Y un de ceux qui apparaissent dans la suite des 7^y.
Bref, tu le fait "complètement à la main"...

[kadaid]

Bonjour
Résoudre 2^x+7^y=4[5] , j'ai choisi 4 au hasard

7=2[5]
Donc on obtient : 2^x+2^y=4[5]
Restes de 2^x et 2^y modulo 5 sont : ={1;2;4;3}
Il y a une seule combinaison :1+3=4
C’est-à-dire 2^x=1[5] ET 2^y=3[5] OU 2^x=3[5] ET 2^y=1[5]

2^4+2^3=4[5]

Donc x=4k-4 ET y=4k-5
S={ 4k-4 ;4k-5}U={ 4k-5 ; 4k-4}

Je n'ai pas mis tous les détails des calculs.

[Lostounet]

Ça me rappelle une fois, j'ai rencontré la notion de "logarithme discret" pour ce genre d'équations (en justifiant bien entendu qu'on peut l'utiliser).
Mais c'est loin du niveau lycée.

[kadaid]

Bonjour
je voulais savoir si ce que j'ai fait est correct et est ce que je peux l'écrire:
S={ 4k-4 ;4k-5}U={ 4k-5 ; 4k-4} équivaut à :
x=-4[4] ET y=-5[4]
Si c'est ça, je remarque le modulo 5 a baissé d'un point.

[Ben314]

Résoudre 2^x+7^y=4[5] , j'ai choisi 4 au hasard
7=2[5]
Donc on obtient : 2^x+2^y=4[5]
Restes de 2^x et 2^y modulo 5 sont : ={1;2;4;3} <= Jusque là, O.K.
Il y a une seule combinaison :1+3=4 <= NON : il y a aussi 2+2=4
C’est-à-dire 2^x=1[5] ET 2^y=3[5] OU 2^x=3[5] ET 2^y=1[5] <= O.K. modulo qu'il manque celles correspondant à 2+2=4

Donc x=4k-4 ET y=4k-5 <= NON : il n'y a pas de raison que ce soit "le même k" pour les deux.
A remplacer par x=4k-4 et y=4j-5, voire même plutôt par x=4k et y=4j+3 vu que x et y doivent être >=0
S={ 4k-4 ;4k-5}U={ 4k-5 ; 4k-4} <= (très) mal écrit : les "solutions" sont des couples (x,y) à mettre entre parenthèses donc l'ensemble des solutions est un ensemble de couples d'entiers et pas un ensemble d'entiers.
Écrit correctement, ça donne
Les entiers x et y sont solutions du problème si et seulement si le couple (x,y) est dans l'ensemble S.
(plus les solutions provenant de 2+2=4)

Sinon, concernant le fait que "le modulo 5 a baissé d'un point", ça correspond à ce que je te disait plus haut (qui est pas mal hors programme niveau Lycée), c'est que les (éventuelles) solutions de avec p premier (par exemple p=5) sont de la forme où l'entier est un diviseur de (si p=5 alors p-1=4 et donc d=1 ou 2 ou 4)

[kadaid]

Bonjour Ben314
Merci pour la correction et je pense que maintenant j'ai compris la méthode au niveau terminale.

Voici un exemple:
9^x+2^y=0[11]
Voici la réponse et cette fois ci j'ai utilisé toutes les combinaisons
Suite des restes de 9^x modulo 11: {1,9,4,3,5}
Suite des restes de 2^y modulo 11: {1,2,4,8,5,10,9,7,3,6}
combinaisons:11={(1+10),(9+2),(4+7),(3+8),(5+6)}

Couples solutions correspondants:
x=1[5] et y=1[10]
x=2[5] et y=7[10]
x=3[5] et y=3[10]
x=4[5] et y=9[10]

Selon la règle que tu as citée:
11 est premier donc le nouveau modulo d divise d est un diviseur de 11-1=10
Ici d={5;10}

Au fait, le modulo 5 on peut le multiplier par 2 pour avoir le même modulo 10 pour x et y, je l'ais essayé et ça marche.
Je pense qu'on peut le montrer comme ça:
x=1[5] équivaut à x=1+5k équivaut à x=1+5(2k) équivaut à x=1+10k' équivaut à x=1[10]

J'espère que je n'ai pas écrit de bêtises dans ce message!

[zygomatique]

Je pense qu'on peut le montrer comme ça:
x=1[5] équivaut à x=1+5k équivaut à x=1+5(2k) équivaut à x=1+10k' équivaut à x=1[10]

J'espère que je n'ai pas écrit de bêtises dans ce message!

que penses-tu de x = 6, 16, 26, ...

[Ben314]

Pour compléter le message de zygo, à part la fin qu'il cite, tout le reste est juste.

[kadaid]

Bonjour

que penses-tu de x = 6, 16, 26, ...

x=5k+1 pour k={1;2;3...}
c'est à dire x=1[5k], avec k={1;2;3...}

Ah oui, le modulo est un multiple de 5, donc on peut choisir k comme on veut pour choisir le modulo qui nous arrange!

[Ben314]

Pas très clair ton dernier post.

x=1[5] équivaut à x=1+5k équivaut à x=1+5(2k) équivaut à x=1+10k' équivaut à x=1[10]

En fait, l'erreur, elle est là (en rouge).
Si x=1+5k et que tu veut regarder modulo 10, ce qu'il faut écrire, c'est que :
- Soit k est pair, donc k=2k' et x=1+5(2k')=1+10k' c'est à dire x congru à 1 modulo 10.
- Soit k est impair, donc k=2k'+1 et x=1+5(2k'+1)=6+10k' c'est à dire x congru à 6 modulo 10.
En bref, (x est congru à 1 modulo 5) <=> (x est congru à 1 ou 6 modulo 10)
(l'implication dans ce sens <= est "évidente" vu que 6 est congru à 1 modulo 5)