Congruence d'une somme de cubes

par **XCallumX** » 08 Mar 2014, 14:49

Bonjour à tous !

Je bloque sur un exercice posé en bonus dans un DM de spécialité maths, le voici :

On se fixe des entiers

tels que :

est congru à 0 mod 9

Montrer que au moins un des

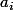
est divisible par 3.

A part faire le tableau de congruences des restes dans les divisions euclidiennes des cubes d'entiers par 9, j'avoue que je suis un peu bloqué, et je n'arrive pas à poursuivre...

Pouvez vous me donner un ou plusieurs petits indices, s'il vous plait ?

Merci

par **Manny06** » 08 Mar 2014, 16:20

XCallumX a écrit:Bonjour à tous !

Je bloque sur un exercice posé en bonus dans un DM de spécialité maths, le voici :

On se fixe des entiers tels que : est congru à 0 mod 9

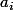
Montrer que au moins un des est divisible par 3.

A part faire le tableau de congruences des restes dans les divisions euclidiennes des cubes d'entiers par 9, j'avoue que je suis un peu bloqué, et je n'arrive pas à poursuivre...

Pouvez vous me donner un ou plusieurs petits indices, s'il vous plait ?

Merci

ai³congru à 0,1,ou -1
on suppose que ai n'est pas congru à 0 donc ai³ n'est pas congru à0
les 7 termes de la somme sont congrus à 1 ou à -1.......peux-tu terminer ?

par **XCallumX** » 08 Mar 2014, 18:04

Manny06 a écrit:ai³congru à 0,1,ou -1
on suppose que ai n'est pas congru à 0 donc ai³ n'est pas congru à0
les 7 termes de la somme sont congrus à 1 ou à -1.......peux-tu terminer ?

Mais d'après ce que vous dite, les 7 termes de la somme sont congrus à 1 ou -1 mais modulo 3 et non modulo 9... Donc je ne comprend pas trop comment passer au modulo 9...

par **Manny06** » 08 Mar 2014, 18:29

XCallumX a écrit:Mais d'après ce que vous dite, les 7 termes de la somme sont congrus à 1 ou -1 mais modulo 3 et non modulo 9... Donc je ne comprend pas trop comment passer au modulo 9...

Montrer que au moins un des a_{i} est divisible par 3.

on fait une demonstration par l'absurde
supposons qu'aucun des ai ne soit divisible par 3
donc ai congru à 1 ou 2 ou 4 ou-4 ou -2 ou-1 mod 9
ai³congru à 1 ou -1 modulo 9 (1³cong1,2³cong-1, 4³cong1,(-4)³cong-1,(-2)³cong1,(-1)³cong-1)

par **Ben314** » 08 Mar 2014, 18:33

là, il faudrait quand même écrire proprement les trucs vu le contexte :

Manny06 a écrit:on suppose que ai n'est pas congru à 0 modulo 3 donc ai³ n'est pas congru à 0 modulo 9

par **Manny06** » 08 Mar 2014, 18:38

Ben314 a écrit:là, il faudrait quand même écrire proprement les trucs vu le contexte :

j'ai déjà rectifié la démonstration

par **XCallumX** » 08 Mar 2014, 18:45

Manny06 a écrit:j'ai déjà rectifié la démonstration

C'est bon j'ai trouvé pareil

Mais après je vois le truc intuitivement, une somme de 7 entiers congrus à 1 ou -1 mod9 ne pourra pas être congrue à 0 mod 9, mais je vois pas comment le démontrer...

par **Manny06** » 08 Mar 2014, 22:42

XCallumX a écrit:C'est bon j'ai trouvé pareil

Mais après je vois le truc intuitivement, une somme de 7 entiers congrus à 1 ou -1 mod9 ne pourra pas être congrue à 0 mod 9, mais je vois pas comment le démontrer...

si tu appelle p le nombre d'entier congru à 1 et 7-p le nombre d'entiers congrus à -1
la somme est congrue à p-(7-p)=2p-7 avec 0<=p<=7
2p-7{-7;-5;-3;-1;1;3;5;7} et ne peut être congru à 0 mod 9

par **nodjim** » 09 Mar 2014, 09:31

Quand tu additionnes un nombre impair de 1 et de -1, peux tu arriver à 0 ?

par **XCallumX** » 09 Mar 2014, 12:46

nodjim a écrit:Quand tu additionnes un nombre impair de 1 et de -1, peux tu arriver à 0 ?

J'avais compris ça intuitivement, mais pour le démontrer j'y arrivais pas ^^

Mais là c'est bon j'ai tout compris

Merci à vous tous !

Congruence d'une somme de cubes

Congruence d'une somme de cubes

Qui est en ligne