[TS Spé] Congruence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 05 Oct 2009, 13:30
par rgabi92 » 05 Oct 2009, 13:30
Bonjour !
Je bloque sur un exo, est ce que vous pourriez m'aider?
1. L'entier n étant supérieur ou égal à 1, montrer que ) est multiple de 5.
est multiple de 5.Donc cela veut dire qu'on doit démontrer que :
)
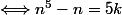
pour k
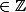
donc


0 [5]
Mais comment faire?
2. En déduire que si p est un entier naturel supérieur ou égal à 1, les nombres 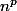 et
et 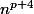 ont même chiffre des unités.
ont même chiffre des unités.
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 05 Oct 2009, 16:28
par rgabi92 » 05 Oct 2009, 16:28
Par classe qu'est ce que tu entends? c'est si n est pair ou impair ?
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 05 Oct 2009, 17:37
par rgabi92 » 05 Oct 2009, 17:37
Si n=0 [5] alors n^4-1 = 4 [5]
Si n=1 [5] alors n^4-1 = 0 [5]
Si n=2 [5] alors n^4-1 = 0 [5]
Si n=3 [5] alors n^4-1 = 0 [5]
Si n=4 [5] alors n^4-1 = 0 [5]
Donc soit n est un multiple de 5, soit n^4-1 est un multiple de 5.
J'ai compris et je sais aussi comment justifier, merci ! :)
Comment en déduire le 2. ?
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 05 Oct 2009, 18:42
par rgabi92 » 05 Oct 2009, 18:42
Les différents chiffres des unités sont :
n=0 [5]
n=1 [5]
n=2 [5]
n=3 [5]
n=4 [5]
non?
Donc n^p = n^(p+5) car c'est cyclique?
J'imagine que c'est l'idée mais comment l'expliquer?
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 05 Oct 2009, 18:57
par rgabi92 » 05 Oct 2009, 18:57
Là je vois pas, j'y réfléchirai demain...
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 06 Oct 2009, 14:15
par rgabi92 » 06 Oct 2009, 14:15
13 873 = 1 387 * 10 + 3
246 753 = 24 675 * 10 + 3
Donc, 13873

3 [10] et 246753

3 [10].
Et 13 873

246 753 [10]
Donc on pourrait exprimer les chiffres des unités en terme de congruence ainsi ? :
n

0 [10]
n

1 [10]
n

2 [10]
n

3 [10]
n

4 [10]
n

5 [10]
n

6 [10]
n

7 [10]
n

8 [10]
n

9 [10]
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 07 Oct 2009, 12:46
par rgabi92 » 07 Oct 2009, 12:46
Petit up ... ^^
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 07 Oct 2009, 13:36
par rgabi92 » 07 Oct 2009, 13:36
On a prouvé precedemment que n^5-n était congru à 0 modulo 5. Comment passer de modulo 5 à modulo 10 ? Je ne pense pas qu'on puisse "juste" multiplier par 2...
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 07 Oct 2009, 13:46
par rgabi92 » 07 Oct 2009, 13:46
15 est un multiple de 5 mais n'est pas un multiple de 10...
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 07 Oct 2009, 13:54
par rgabi92 » 07 Oct 2009, 13:54
Pour qu'un nombre soit multiple de 10, il faut qu'il soit multiple de 5 et de 2. Donc il faudrait prouver que n^5-n est également congru à 0 modulo 2 ?
-
rgabi92
- Membre Naturel
- Messages: 33
- Enregistré le: 06 Sep 2009, 13:03
-
 par rgabi92 » 07 Oct 2009, 14:00
par rgabi92 » 07 Oct 2009, 14:00
C'est bon, j'ai prouvé que n(n^4-1) était congru à 0 modulo 2.
Ai je le droit de dire que comme n^5-n = 5k (pour tout entier k) et n^5-n = 2k alors n^5-n = 10k ?
-
mathelot
 par mathelot » 07 Oct 2009, 14:07
par mathelot » 07 Oct 2009, 14:07
bonsoir,
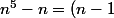n(n+1)(n^2+1))
si l'un des trois entiers consécutifs n-1,n,n+1 est multiple de 5, c'est fini.
sinon n-2 ou n+2 est multiple de 5 alors
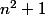
aussi, congru à

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
 0 [5]
0 [5]