Congruence

[virus81]

Bonjour, je travaille sur un devoir maison de spécialité math et je suis pas sure d'avoir vraiment compris la question.
Pourriez vous me confirmer la démarche que j'ai adopte svp:

Etant donné un entier naturel n>2 ou n=2, on se propose d'étudier l'existance de trois entiers naturels x, y et z tels que:
xcarré+ycarré+zcarré congrus 2 exposant n -1 modulo 2 exposant n.

1)Dans cette question , on suppose n=2
Montrer que 1,3 et 5 satisfont à la condition précédente.

réponse: Si n=2: 1+9+25 congrus 3 modulo 4
donc 1+9+25-3=k4 k appartenant à Z
32=k4 or 32/4=8.
donc 1,3 et 5 satisfont à la condition précédente.

[axiome]

Euh, c'est bien que tu veux dire ? Pour pas qui y est de confusion...

[virus81]

Oui c'est bien ca.

[axiome]

Ben, je comprends pas trop ta réponse...
Tu as pour n=2, la donnée devient :
. D'où il sort ton congru 3 ?

[virus81]

j'ai 3 puisque c'est 2exposant 2=4
4-1=3 car c'est (2 exposant n)-1

[axiome]

Ok, ton 1 n'est pas en exposant... Ca change tout, j'avais mal compris...
Ta donnée est donc pour n=2 :

Tu remplaces n par 2 dans celle de départ qui est finalement :

sans 1 en exposant !

[axiome]

Bon, dans ce cas là, ta réponse est juste.

Calcule simplement, c'est plus propre :

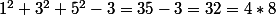
donc
donc 1, 3 et 5 satisfont à la condition précédente.

[virus81]

oui exact. Je suis désolée je n'est aucun symbole sur mon clavier :s

[axiome]

Utilise LaTeX pour faire des symbôles : y a un tuto très bien fait dans la rubrique lycée.

[virus81]

d'accord merci beaucoup. ma réponse est elle juste?

[axiome]

J'ai rédigé comme il faut la réponse (la tienne était juste mais un peu bizarre) au-dessus :
C'est facile à faire.
Pour démontrer que , tu calcules a-b et tu montres que c'est divisible par n (théorème fondamental sur les congruences).

[axiome]

J'ai rédigé comme il faut la réponse au-dessus (la tienne était juste mais un peu bizarre).
C'est facile à faire.
Pour démontrer que , tu calcules simplement a-b et tu montres que c'est divisible par n (théorème fondamental sur les congruences).
@+