Bonjour,
J'ai un exercice à faire et je n'arrive pas à une question. Pouvez-vous m'aider svp ?
Déterminer tous les entiers n tels que n²+n+4 ≡ 0[15].
Merci
Congruence Arithmétique
8 messages
- Page 1 sur 1
Re: Congruence Arithmétique
Bonjour,
une méthode (je ne sais pas si c'est celle qui est attendue) peut être de factoriser le trinôme en le mettant d'abord sous forme canonique.
Tu vas devoir "diviser par 2" c'est à dire trouver l'inverse a de 2 modulo 15.
Dans ce cas n²+n = n²+2an = n²+2an+a²-a² = (n+a)²-a² [15].
une méthode (je ne sais pas si c'est celle qui est attendue) peut être de factoriser le trinôme en le mettant d'abord sous forme canonique.
Tu vas devoir "diviser par 2" c'est à dire trouver l'inverse a de 2 modulo 15.
Dans ce cas n²+n = n²+2an = n²+2an+a²-a² = (n+a)²-a² [15].
Re: Congruence Arithmétique
Sinon, il y a plus simple, il suffit de tester toutes les valeurs de n entre 0 et 14.
Re: Congruence Arithmétique
Bonjour
Je ne prétends pas que cette solution soit la plus rapide mais elle fonctionne...
On cherche n tel que n²+n+4=15k avec k entier
ou n²+n+4-15k=0
Le discriminant D est tel que
D=1-4(4-15k)=60k-15
Pour que n soit entier il faut que D soit le carré d'un entier p
On a donc 60k-15=p²,
p doit être multiple de 15 puisque 15 divise 60k-15
donc 60k-15=(15q)²=225q²
ou 4k-1=15q ou 4k=15q+1
(Equation diophantienne à résoudre pour avoir toutes les valeurs possibles de k et donc de D puis n)
Par ex, pour q=1, on a une solution puisque k=4 et D=225 et n =7 ou n=-8
Je ne prétends pas que cette solution soit la plus rapide mais elle fonctionne...
On cherche n tel que n²+n+4=15k avec k entier
ou n²+n+4-15k=0
Le discriminant D est tel que
D=1-4(4-15k)=60k-15
Pour que n soit entier il faut que D soit le carré d'un entier p
On a donc 60k-15=p²,
p doit être multiple de 15 puisque 15 divise 60k-15
donc 60k-15=(15q)²=225q²
ou 4k-1=15q ou 4k=15q+1
(Equation diophantienne à résoudre pour avoir toutes les valeurs possibles de k et donc de D puis n)
Par ex, pour q=1, on a une solution puisque k=4 et D=225 et n =7 ou n=-8
Re: Congruence Arithmétique
Bonsoir,
modulo 3, on obtient:



^2 \equiv 0 [3])

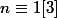
modulo 5, on obtient:



^2 \equiv 0 [5])


on applique ensuite le théorème des restes chinois.
https://fr.wikipedia.org/wiki/Th%C3%A9o ... %20nombres.
modulo 3, on obtient:
modulo 5, on obtient:
on applique ensuite le théorème des restes chinois.
https://fr.wikipedia.org/wiki/Th%C3%A9o ... %20nombres.
Re: Congruence Arithmétique
Je me rends compte que j'ai commis une erreur dans mon message précédent , je corrige :
Ce qui fait que l'on peut seulement donner comme solution l'exemple n=7 ou n=-8
Toutefois si on ajoute un multiple de 15 à ces exemples on obtient d'autres solutions (se démontre facilement)
catamat a écrit:donc 60k-15=(15q)²=225q²
ou 4k-1=15q² ou 4k=15q²+1
Ce qui fait que l'on peut seulement donner comme solution l'exemple n=7 ou n=-8
Toutefois si on ajoute un multiple de 15 à ces exemples on obtient d'autres solutions (se démontre facilement)
Re: Congruence Arithmétique
mathelot a écrit:Bonsoir,
modulo 3, on obtient:
modulo 5, on obtient:
on applique ensuite le théorème des restes chinois.
https://fr.wikipedia.org/wiki/Th%C3%A9o ... %20nombres.
avec les notations de l'article du wiki sur le théorème des restes chinois:
on doit résoudre le système d'inconnue n
On pose
il vient
d'après (1) :
On pose
il vient
d'après (1) :
ce qui donne une solution particulière du système
d'où la solution générale
Re: Congruence Arithmétique
autre méthode:
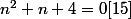
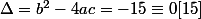
d'où une racine double:
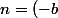/2a \equiv -1 \times 2^{-1} \equiv -8 \equiv 7 [15])
on vérifie que
^2\equiv n^2+n+4 [15])
d'où
^2 \equiv 0 [15])
Les diviseurs de zéro et
et  ne donnent pas de solutions.
ne donnent pas de solutions.
reste la solution
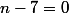
d'où
d'où une racine double:
on vérifie que
d'où
Les diviseurs de zéro
reste la solution
d'où
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
