Confirmation solution arithmétique

[J-R]

bonjour,

je voudrais des remarques sur ma solution:

énoncé:

soit a et b deux entiers naturels tel que la somme soit un multiple de leur produit.

a+b=kab,

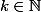
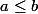
je supoose que (ai-je le droit ?)

donc

=>

=>

les seules possiblité sont donc a=1 et k=2 donc b=1; ou a=2 et k=1 donc b=2.

voilà

merci

[emdro]

bonjour J-R,

comme le problème est symétrique en a et b (somme, produit), tu peux tout à fait choisir de baptiser a le plus petit.

De kab<=2b à ka<=2, il me semble que tu as divisé par b.
b est bien positif (dans IN), mais s'il était nul?
C'est un cas supplémentaire à envisager.

Sinon, c'est bon. :happy2:

[Flodelarab]

Il manque 0. non ?

[emdro]

Oui, c'est vrai que 0<2 , donc a priori, cela manquait dans le raisonnement: ka<=2

(Mais si a=0, et a+b est multiple de ab, alors b=0 aussi, et ce cas a été évincé par la simplification scandaleuse par b)!

[J-R]

ah oui d'accord faut que je fasse gaffe à ca :doh:

merci

sinon pour ma demande: en fait si c'est commutatif alors je peux choisir a et b comme je veux ?

[emdro]

Oui, c'est juste un nom de baptême; si par hasard, a était plus grand que b, il suffirait d'inverser les notations!

[J-R]

ok ca marche

merci

a+

[Flodelarab]

ah oui d'accord faut que je fasse gaffe à ca :doh:

merci

sinon pour ma demande: en fait si c'est commutatif alors je peux choisir a et b comme je veux ?

Tu trouveras 2 fois plus de cas si tu ne mets pas a et b dans l'ordre. Rien de faux.