Compréhension inéga
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Jan 2011, 16:04
par nee-san » 15 Jan 2011, 16:04
bonjour alors j'aurais besoin d'aide pour savoir comment lorsque que l'on doit démontrer que:
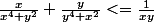
comment passe t'on à la:

voila merci à vous
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 15 Jan 2011, 16:20
par XENSECP » 15 Jan 2011, 16:20
A vue de nez, plus de "contexte" serait bienvenue pour bien comprendre le sujet !
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Jan 2011, 16:43
par nee-san » 15 Jan 2011, 16:43
XENSECP a écrit:A vue de nez, plus de "contexte" serait bienvenue pour bien comprendre le sujet !
ba c'était juste démontrer que
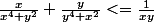
et j'ai pas compris comment passe t'on a la seconde ligneet aussi x et y supérieur à 0
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 15 Jan 2011, 16:56
par XENSECP » 15 Jan 2011, 16:56
Lol ! Comme ça ? Sans plus d'infos sur x et y ?
Je trouve ça assez léger !
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Jan 2011, 16:58
par nee-san » 15 Jan 2011, 16:58
XENSECP a écrit:Lol ! Comme ça ? Sans plus d'infos sur x et y ?
Je trouve ça assez léger !
ba oui on sais juste que x et y sont supérieur à 0

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 15 Jan 2011, 16:59
par Sa Majesté » 15 Jan 2011, 16:59
Comme tu fais l'effort d'écrire en TEX, je t'informe que supérieur ou égal s'écrit \geq et inférieur ou égal s'écrit \leq

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Jan 2011, 17:09
par Olympus » 15 Jan 2011, 17:09
Salut !
Soient
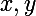
deux éléments de
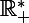
.
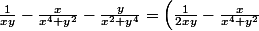+\left( \frac{1}{2xy}-\frac{y}{x^2+y^4} \right) = \frac{1}{2xy}\left(\frac{x^4+y^2-2x^2y}{x^4+y^2}+\frac{x^2+y^4-2xy^2}{x^2+y^4}\right)=\frac{1}{2xy}\left( \frac{\left(x^2-y\right)^2}{x^4+y^2} + \frac{ \left(x-y^2\right)^2 }{x^2+y^4}\right) \geq 0)
Avec égalité ssi
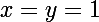
.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Jan 2011, 18:57
par Olympus » 15 Jan 2011, 18:57
Re,
la deuxième inégalité est fausse par contre ( prend x=y=1 ), ou alors mal recopiée.
-
tarask
- Messages: 3
- Enregistré le: 04 Déc 2010, 19:31
-
 par tarask » 15 Jan 2011, 19:12
par tarask » 15 Jan 2011, 19:12
Pour la première inégalité , c'est un peu trivial sans avoir recourt au calcul .
on sait d'après IAG que [img]http://latex.codecogs.com/gif.latex?x^2+y^4\geq%202y^2x[/img] ce qui donne immédiatement [img]http://latex.codecogs.com/gif.latex?\frac{y}{x^2+y^4}\leq%20\frac{1}{2xy}[/img] on fait cela deux fois pour obtenir l'inégalité désirée .
Sauf erreur et merci .

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Jan 2011, 19:18
par Olympus » 15 Jan 2011, 19:18
Sous forme de somme de carrés ça fait plus classe ^^
PS : c'est le même principe qui est utilisé sinon, si tu développes
^2)
tu tombes sur ton application de l'IAG

-
tarask
- Messages: 3
- Enregistré le: 04 Déc 2010, 19:31
-
 par tarask » 15 Jan 2011, 19:25
par tarask » 15 Jan 2011, 19:25
Olympus a écrit:Sous forme de somme de carrés ça fait plus classe ^^
PS : c'est le même principe qui est utilisé sinon, si tu développes
^2)
tu tombes sur ton application de l'IAG

Certes !
parce que parfois , et dans quelques solutionnaires d'inégalités , on parachute des carrés comme ça ... (surtout la méthode SOS

)
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Jan 2011, 19:43
par nee-san » 15 Jan 2011, 19:43
Olympus a écrit:Re,
la deuxième inégalité est fausse par contre ( prend x=y=1 ), ou alors mal recopiée.
et si x et y sont diéffrent mais positif car ds un site ils sont passer de la premiere à la seconde

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Jan 2011, 19:48
par Olympus » 15 Jan 2011, 19:48
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Jan 2011, 21:45
par nee-san » 15 Jan 2011, 21:45
ok mais je viens de voir si animath qu'il y avait ma même inégalité et j'ai pas compris le raisonnement
sinon bonsoir et merci à vous deux

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Jan 2011, 21:51
par Olympus » 15 Jan 2011, 21:51
Si tu parles de la page 5 d'Animath, alors tu as bel et bien mal recopié la deuxième inégalité. Compare ton premier post avec cet extrait d'Animath :

Sinon, ce qu'ils ont fait est juste une simple application de AM-GM, comme l'a montré tarask.
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Jan 2011, 21:56
par nee-san » 15 Jan 2011, 21:56
tu peut me dire c quoi iag car je trouve plus et merci encore c vrai j'ai mal copier

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Jan 2011, 22:01
par Olympus » 15 Jan 2011, 22:01
nee-san a écrit:tu peut me dire c quoi am-gm car je trouve plus et merci encore c vrai j'ai mal copier
Euh je te l'ai dit y a quelques semaines ^^' Sinon, c'est juste l'inégalité
 \in \mathbb{R}^2 \qquad : \qquad x^2+y^2 \geq 2xy)
, ou de manière équivalente
 \in \mathbb{R}_+^2 \qquad : \qquad x+y \geq 2\sqrt{xy})
. C'est le "Théorème 2" page 5 dans ton cours Animath :lol3:
Le cas général ( AM-GM ) s'énonce comme suit :
 \in \mathbb{R}_+^n \qquad : \qquad \bigsum_{k=1}^n x_k \geq \left( \bigprod_{k=1}^n x_k \right)^{\frac{1}{n}})
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Jan 2011, 22:06
par nee-san » 15 Jan 2011, 22:06
Olympus a écrit:Euh je te l'ai dit y a quelques semaines ^^' Sinon, c'est juste l'inégalité
 \in \mathbb{R}^2 \qquad : \qquad x^2+y^2 \geq 2xy)
, ou de manière équivalente
 \in \mathbb{R}_+^2 \qquad : \qquad x+y \geq 2\sqrt{xy})
. C'est le "Théorème 2" page 5 dans ton cours Animath :lol3:
ah ok j'avais pas compris que c'était ça ba merci bien de l'aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
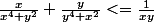
 voila merci à vous
voila merci à voustu tombes sur ton application de l'IAG

